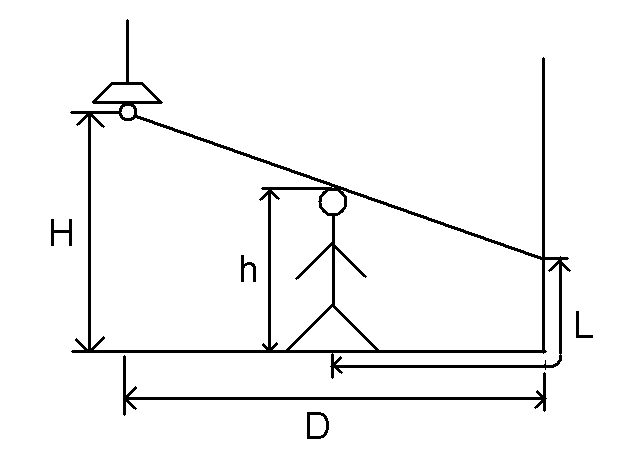
题意：多组数据。一个房间里有个灯泡，灯的高度为 H\text{H}，人的高度为 hh，房间宽度为 D\text{D}，求影子长度 L\text{L} 的最大值。

房间

数据范围与约定：

1≤T≤100,10−2≤H,h,D≤103,H−h≥10−21\le T\le 100,10 ^{-2}\le \text{H},h,\text{D}\le 10 ^{3},\text{H}-h\ge 10 ^{-2}。

解析：这道题其实可以靠推数学公式做的，但是这里着重介绍三分法。

可以发现，人从灯正下方向墙移动，投影在墙上的影子长度递增，而投影在地上的影子长度递减，加起来是一个单峰函数，我们可以三分解决。

现在的问题就是要获知影子长度 L\text{L} 与人离灯的距离 xx 的函数关系。

首先我们算地上影子的长度，这个易知是 D−x\text{D}-x；

然后算墙上影子的长度，我们假象在灯和影子最高点处作墙的垂线，如图所示：

作垂线后

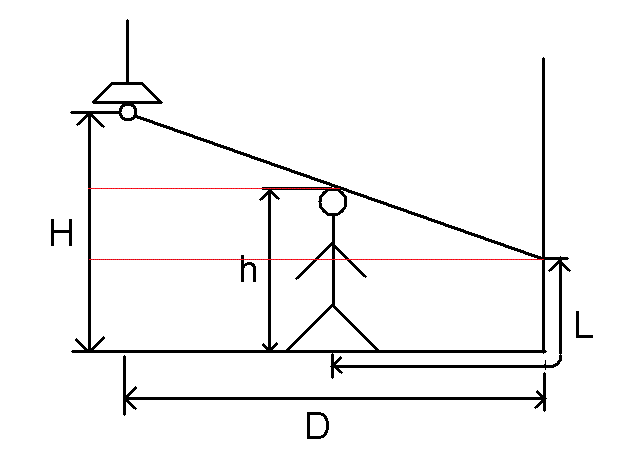
这两个三角形相似，根据比例关系，墙上影子的高度为：

H−(H−h)⋅Dx\text{H}-(\text{H}-h)\cdot\dfrac{\text{D}}{x}

所以影子长度的关系式为：

L=(D+H−x)−(H−h)⋅Dx\text{L}=(\text{D}+\text{H}-x)-(\text{H}-h)\cdot\dfrac{\text{D}}{x}

实际上这是个对勾函数，可用数学方法直接计算答案。我们采用三分法，但是要注意定义域的问题。一开始是没有墙上的影子的，地上的影子随着向墙移动长度递增，直到投影点与墙角重合时达到最值。很明显只有地上影子的一段不可能是最优的，所以我们可以更新下限，下限为投影点与墙角重合时人离灯的距离，同理运用相似三角形：

min⁡x=D⋅H−hH\min x=\text{D}\cdot \dfrac{\text{H}-h}{\text{H}}

所以定义域为 [D⋅H−hH,D][\text{D}\cdot \dfrac{\text{H}-h}{\text{H}},\text{D}]，从这里开始三分即可。

#include<stdio.h>
int t;
double H,h,D,eps=1e-9;
double count(double x)
{
	double L=(D-x+H)-(H-h)*D/x;
	return L;
}
double three_devide(double l,double r)
{
	double f1,f2,mid,mmid;
	while(r-l>=eps)
	{
		mid=l+(r-l)/3;
		mmid=r-(r-l)/3;
		f1=count(mid);
		f2=count(mmid);
		if(f1>=f2)
			r=mmid;
		else
			l=mid;	
	}
	return f1;
}
int main()
{
	int i,j;
	scanf("%d",&t);
	while(t--)
	{
		scanf("%lf%lf%lf",&H,&h,&D);
		printf("%.3lf\n",three_devide((H-h)*D/H,D));
	}
	return 0;
}