题意:P 教授有编号为 的 件玩具,第 件玩具经过压缩后的一维长度为 。为了方便整理,P 教授要求:
- 在一个一维容器中的玩具编号是连续的。
- 同时如果一个一维容器中有多个玩具,那么两件玩具之间要加入一个单位长度的填充物。形式地说,如果将第 件玩具到第 个玩具放到一个容器中,那么容器的长度将为 。
制作容器的费用与容器的长度有关,根据教授研究,如果容器长度为 ,其制作费用为 。其中 是一个常量。P 教授不关心容器的数目,他可以制作出任意长度的容器,甚至超过 。但他希望所有容器的总费用最小。
数据结构与约定:对于所有数据,满足 。
解析:建议在学习斜率优化之前先了解单调队列优化 DP。
我们可以知道,对于这种 的这种式子,用单调队列可以优化到线性复杂度。
但是如果形如 这种带有乘法的式子,由于 这一项既与 有关又与 有关,所以不能考虑单调队列优化了,这就要用到我们今天学的斜率优化了。
来看看这道题,我们设 为前 个玩具所花费的最小价值, 为 的前缀和,可以得到状态转移方程为:
表示将第 的玩具用一个容器装起来。
我们把包含 和 的式子分开,即令 ,可以得到:
拆开得到:
移项得到:
我们令 ,令 ,这个式子就可以看作一条斜率为 的直线。
接下来是一个无比重要的性质:
如果 且 ,那么 比 更优,否则 比 更优。即斜率的单调性。
证明:
我们假设 比 更优,且 。那么:
展开再移项得:
即:
故:
假设成立,得证。
假设在这个平面坐标系上存在点 和 ,那么 就是两点间连线的斜率,我们用 表示 两点的斜率。
接下来也是一个非常重要的性质:
坐标系上,每次决策时可能选取的最优的点组成了一个下凸包,即相邻两点斜率单调递增。
证明:
依然采用假设法,同时采用反证法。
假设有三个点 ,满足 。假设 ,即下面这个样子(上凸包的情况):
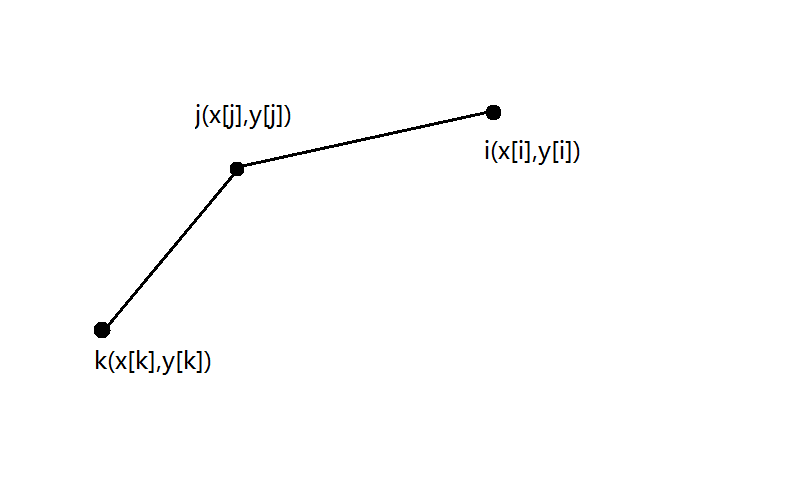
那么 有三种关系:
- 当 时,由第一个性质可知, 比 优, 比 优, 不是最优;
- 当 时,同理, 比 优, 比 优, 不是最优;
- 当 时,同理, 比 优, 比 优, 不是最优。
即无论如何 都不是最优,即这种情况可以排除了。
所以我们需要维护一个下凸包,即 ,如下图:
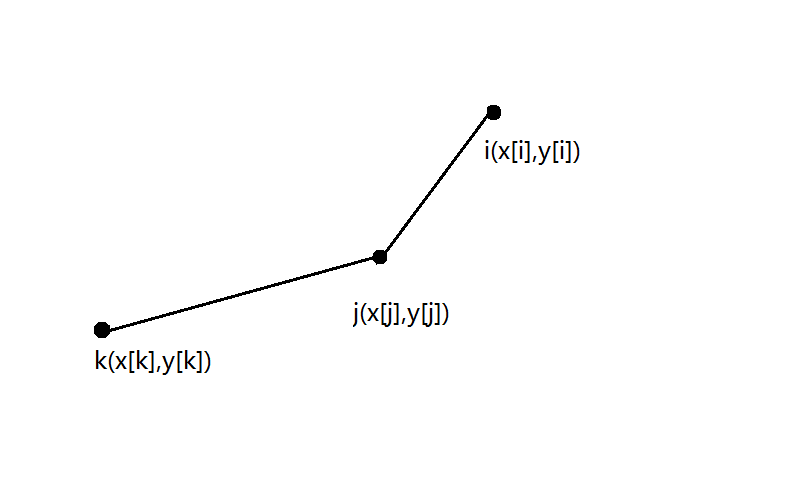
即下凸包的斜率永远单调递增,可以用单调队列来维护这个凸包,由两个性质可得,最优点就是下凸包中第一个斜率大于 的点。
我们维护每个可能的最优点,首先第一步,取出最优的点,即每次在队头判断是否 ,因为最优点是下凸包中斜率大于 的点,所以如果小于 就弹出队头;
第二步按照转移方程更新 点的 值即可;
第三步就是维护斜率的单调递增,判断 这个点是否可以被加入下凸包,即要使得 ,所以弹出所有满足 的队尾;
第四步将 入队即可。
最终 即是答案。
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<ctime>
#define INF 1e9
using namespace std;
const int maxn=50010;
int n,l;
int head,tail,q[maxn];
double sum[maxn],f[maxn];
double a(int i)
{
return sum[i]+i;
}
double b(int i)
{
return a(i)+l+1;
}
double x(int i)
{
return b(i);
}
double y(int i)
{
return f[i]+b(i)*b(i);
}
double slope(int i,int j)
{
return (y(i)-y(j))/(x(i)-x(j));
}
int main()
{
scanf("%d%d",&n,&l);
for(int i=1;i<=n;i++)
{
scanf("%lf",&sum[i]);
sum[i]+=sum[i-1];
}
head=1;
tail=1;
for(int i=1;i<=n;i++)
{
while(head<tail&&slope(q[head],q[head+1])<2*a(i))//保持单调最优性
head++;
f[i]=f[q[head]]+(a(i)-b(q[head]))*(a(i)-b(q[head]));
while(head<tail&&slope(i,q[tail])<slope(q[tail-1],q[tail]))//维持斜率单调递增,下凸包
tail--;
q[++tail]=i;
}
printf("%lld",(long long)f[n]);
return 0;
}
