NOIP2020 解析

被 T1 坑了 $30$ 分，来补题了。

T1 排水系统

解析：可以看出就一个裸的拓扑排序，用结构体维护分数然后暴力转移就行了。但是注意要高精度！！！假设最后某个汇点有三条路到达，每条路都是极限情况只分不汇，那么分母各为 $2 ^{11},3 ^{11}, 5 ^{11}$ ，最终的分母就是 $60 ^{11}$ ，会超 long long，所以最后 $10$ pts 要写高精度。

同时在转移分数的时候，通分一定要先除后乘！！！先乘后除的话可能一开始就会爆出 long long，然后你就会和我一样挂成 $60$ pts。

这里懒得写高精度，所以用了 __int128 来实现。

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<queue>
#define INF 1e9
#define ll __int128
using namespace std;
const int maxn=500010;
int n,m;
int head[maxn],cnt;
int indeg[maxn],oudeg[maxn];
struct node
{
	int next;
	int to;
}e[maxn<<1];
inline void add(int from,int to)
{
	e[++cnt].next=head[from];
	e[cnt].to=to;
	head[from]=cnt;
}
struct fac
{
	ll x;
	ll y;
}ans[maxn];
ll gcd(ll a,ll b)
{
	if(!b)
		return a;
	return gcd(b,a%b);
}
inline ll lcm(ll a,ll b)
{
	return a/gcd(a,b)*b;
}
fac inc(fac a,fac b)
{
	ll p=lcm(a.y,b.y);
	ll num1=p/a.y*a.x;
	ll num2=p/b.y*b.x;
	num1+=num2;
	num2=p;
	ll num=gcd(max(num1,num2),min(num2,num1));
	return (fac){num1/num,num2/num};
}
fac chu(fac a,ll o)
{
	ll num1=a.x;
	ll num2=a.y*o;
	ll num=gcd(max(num1,num2),min(num2,num1));
	return (fac){num1/num,num2/num};
}
queue<pair<int,fac> > q;
inline void write(ll x)
{
	if(!x)
		return ;
	if(x>9)
		write(x/10);
	putchar(x%10+'0');
}
int main()
{
	freopen("water.in","r",stdin);
	freopen("water.out","w",stdout);
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
	{
		int x;
		scanf("%d",&x);
		for(int j=1;j<=x;j++)
		{
			int p;
			scanf("%d",&p);
			add(i,p);
			indeg[p]++;
			oudeg[i]++;
		}
	}
	for(int i=1;i<=n;i++)
	{
		ans[i].y=1ll;
		if(!indeg[i])
		{
			ans[i]=(fac){1ll,1ll};
			q.push(make_pair(i,ans[i]));
		}	
	}
	while(!q.empty())
	{
		int u=q.front().first;
		fac now=q.front().second;
		q.pop();
		for(int i=head[u];i;i=e[i].next)
		{
			int v=e[i].to;
			fac p=chu(now,(__int128)oudeg[u]);
			ans[v]=inc(ans[v],p);
			indeg[v]--;
			if(!indeg[v])
				q.push(make_pair(v,ans[v]));
		}
	}
	for(int i=1;i<=n;i++)
		if(!oudeg[i])
		{
			write(ans[i].x);
			printf(" ");
			write(ans[i].y);
			printf("\n");
		}
	return 0;
}
/*
5 1
3 2 3 5
2 4 5
2 5 4
0
0
*/

T2 字符串匹配

解析：芜湖，CCF 考字符串了，爷青结。

这个 T2 先乍一看不会，但是仔细想想就会发现其实可做。考场上写了 $O(n\sqrt {n})$ 的做法拿了 $84$ 。这个做法是用的 KMP 算法加枚举约数。首先先 $O(n)$ 枚举 $(\text{AB}) ^{k}$ 与 $\text{C}$ 的分界点 $i$ ，然后再算出 $s _{1\sim i}$ 能分成多少种不同的 $(\text{AB}) ^{k}$ 的情况。我们可以用 KMP 算法 $O(1)$ 求出前面这一坨的最小循环节长度为 $len$ ，那么 $\text{AB}$ 的长度肯定是它的倍数，发现这时候枚举倍数最坏复杂度为 $O(n)$ ，那么总复杂度就为 $O(n ^{2})$ 了，不可取。我们换种方法枚举，由于最小循环节长度为 $len$ ，那么它的数量就为 $\dfrac{i}{len}$ ，由于 $\text{AB}$ 肯定由几个最小循环节连在一起组成，所以 $\text{AB}$ 的数量肯定是 $\dfrac{i}{len}$ 的约数，直接 $O(\sqrt{n})$ 枚举约数即可。如果这个串没有最小循环节，那么只用算这整个串为 $\text{AB}$ 的贡献即可。最后还有一个出现奇数次的字符数量的限制，我们直接预处理前缀与后缀出现了奇数次的字符的数量，然后 $O(26n)$ 统计出前缀 $1\sim i$ 中有多少个前缀出现了奇数次的字符的数量小于等于 $j$ ，然后在算贡献的时候直接加即可。

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<vector>
#define INF 1e9
using namespace std;
const int maxn=(1<<20)+5;
int t,n,nex[maxn];
char s[maxn];
int pre[maxn],sub[maxn],num[27];
long long ans,sum[maxn][27];
int main()
{
	//freopen("string.in","r",stdin);
	//freopen("string.out","w",stdout);
	scanf("%d",&t);
	while(t--)
	{
		ans=0;
		scanf("%s",s+1);
		n=strlen(s+1);
		pre[0]=sub[n+1]=0;
		memset(num,0,sizeof(num));
		for(int i=1;i<=n;i++)
		{
			int c=s[i]-'a'+1;
			num[c]++;
			if(num[c]&1)
				pre[i]=pre[i-1]+1;
			else
				pre[i]=pre[i-1]-1;
		}
		memset(num,0,sizeof(num));
		int maxx=0;
		for(int i=n;i>=1;i--)
		{
			int c=s[i]-'a'+1;
			num[c]++;
			if(num[c]&1)
				sub[i]=sub[i+1]+1;
			else
				sub[i]=sub[i+1]-1;
			maxx=max(maxx,sub[i]);
		}
		for(int j=0;j<=maxx;j++)
			sum[0][j]=0ll;
		for(int i=1;i<=n;i++)
		{
			for(int j=0;j<pre[i];j++)
				sum[i][j]=sum[i-1][j];
			for(int j=pre[i];j<=maxx;j++)
				sum[i][j]=sum[i-1][j]+1;
		}
		nex[1]=0;
		for(int i=2,j=0;i<=n;i++)
		{
			while(j>0&&s[i]!=s[j+1])
				j=nex[j];
			if(s[i]==s[j+1])
				j++;
			nex[i]=j;
		}
		for(int i=2;i<n;i++)
		{
			int p=sub[i+1];
			int j=nex[i];
			int len=0;
			if(i%(i-j)==0&&j)
				len=i-j;
			else
				len=0;
			if(!len)
				ans+=sum[i-1][p];
			else
			{
				int num=i/len;
				int lim=sqrt(num);
				for(int j=1;j<=lim;j++)
					if(num%j==0)
					{
						int now=j*len;
						ans+=sum[now-1][p];
						if(j*j!=num)
						{
							int nnow=num/j*len;
							ans+=sum[nnow-1][p];
						}
					} 
			}
		}
		printf("%lld\n",ans);
	}
	return 0;
}

然后针对这个算法改进，我们把枚举约数改为枚举倍数，所以时间复杂度降为调和级数复杂度为 $O(n\log n)$ ，可能是因为常数过大的原因只能拿到 $92$ pts。

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<vector>
#define INF 1e9
using namespace std;
const int maxn=(1<<20)+2;
int t,n,nex[maxn];
char s[maxn];
int sub[maxn],num[27];
long long ans,sum[maxn][27];
int main()
{
	//freopen("string.in","r",stdin);
	//freopen("string.out","w",stdout);
	scanf("%d",&t);
	while(t--)
	{
		ans=0;
		scanf("%s",s+1);
		n=strlen(s+1);
		sub[n+1]=0;
		memset(num,0,sizeof(num));
		int maxx=0;
		for(int i=n;i>=1;i--)
		{
			int c=s[i]-'a'+1;
			num[c]++;
			if(num[c]&1)
				sub[i]=sub[i+1]+1;
			else
				sub[i]=sub[i+1]-1;
			maxx=max(maxx,sub[i]);
		}
		for(int j=0;j<=maxx;j++)
			sum[0][j]=0ll;
		memset(num,0,sizeof(num));
		int last=0,now=0;
		for(int i=1;i<=n;i++)
		{
			int c=s[i]-'a'+1;
			num[c]++;
			if(num[c]&1)
				now=last+1;
			else
				now=last-1;
			for(int j=0;j<now;j++)
				sum[i][j]=sum[i-1][j];
			for(int j=now;j<=maxx;j++)
				sum[i][j]=sum[i-1][j]+1;
			last=now;
		}
		nex[1]=0;
		for(int i=2,j=0;i<=n;i++)
		{
			while(j>0&&s[i]!=s[j+1])
				j=nex[j];
			if(s[i]==s[j+1])
				j++;
			nex[i]=j;
		}
		for(int i=2;i<n;i++)
			for(int j=1;j<=n/i;j++)
			{
				int allen=i*j;
				if(allen>=n)
					continue;
				int k=nex[allen];
				int p=sub[allen+1];
				int len=0;
				if(allen%(allen-k)==0&&k)
					len=allen-k;
				else
					len=0;
				if(!len)
				{
					if(j==1)
						ans+=sum[allen-1][p];
					continue;
				}
				else if(i%len==0)
					ans+=sum[i-1][p];
			}
		printf("%lld\n",ans);
	}
	return 0;
}

正解我是用 Z 函数，即扩展 KMP 算法做的，时间复杂度也是 $O(n\log n)$ ，但是常数十分优秀。Z 函数是一个十分高效的算法，它能在 $O(n)$ 的时间复杂度内计算出 $z _{i}$ ，代表以 $s _{i}$ 开头的后缀与整个字符串 $s$ 的 LCP 长度。Z 函数的应用和 KMP 几乎完全一样，但是它的实现方式却与 Manacher 算法类似，都属于势能分析一块。我们对于每一个下标 $i$ ，称 $[i,i+z _{i}-1]$ 是 $i$ 的匹配段，即 Z-box，初始值我们令 $z _{1}=0$ ，然后从 $2$ 开始计算 $z _{i}$ 。我们维护右端点最靠右的匹配段 $[l,r]$ ，易知 $s _{1\sim r-l+1}=s _{l\sim r}$ ，初始 $l=1,r=0$ ，然后在计算 $z _{i}$ 时，如果 $i\le r$ ，即 $i$ 在匹配段中，那么 $z _{i}$ 至少为 $\min(z _{i-l+1},r-i+1)$ ，于是我们就把 $z _{i}$ 赋为这个值，再用朴素算法向外扩展即可，如果 $i>r$ 就直接朴素向外扩展，最后求出 $z _{i}$ 后要记住更新区间 $[l,r]$ 。计算完 $z _{i}$ 后，在根据题目考虑要不要把 $z _{1}$ 赋值为 $n$ ，即整个字符串长度(从定义出发)。

这道题，我们先预处理出 $sub _{i}$ 代表 $s _{i\sim n}$ 中的奇数字符的个数，然后在求 $z _{i}$ 的过程中统计答案，并且同时计算出 $1\sim i$ 中的奇数字符个数为 $pre$ 的位置个数 $cnt _{pre}$ ，然后对于每一个 $i>2$ 的位置，先用 $sum$ 数组算出 $cnt$ 的前缀和，即 $1\sim i$ 中奇数字符个数小于等于 $i$ 的位置个数 $sum _{i}$ ，统计答案时我们将 $1\sim i-1$ 看作 $\text{AB}$ ，那么 $(\text{AB}) ^{k}$ 即为 $lim=\min(n-1,i+z _{i}-1)$ ，所以 $k\in [1,\dfrac{lim}{i-1}]$ ，所以 $\text{C}$ 的下标为 $(i-1)\times k+1\sim n$ ，我们加上 $sum _{sub _{(i-1)\times k+1}}$ 即可，复杂度最坏为 $O(\log n)$ ，故总复杂度最坏也为 $O(n\log n)$ ，但由于上界 $lim$ 的原因，实际会比这个复杂度快很多。

/*
 * @Author: clorf 
 * @Date: 2020-12-10 22:23:40 
 * @Last Modified by: clorf
 * @Last Modified time: 2020-12-10 22:45:26
 */
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<ctime>
#include<cctype>
#define INF 2e9
using namespace std;
const int maxn=(1<<20)+2;
const double Pi=acos(-1.0);
const double eps=1e-7;
//1.数组开小
//2.没用long long/爆了类型存储范围
//3.写之前式子没推清楚
//4.变量写错(想当然typo/没想清楚含义)
//5.写之前没想清楚复杂度
//6.常量数字与long long连用时要加ll！！！
//7.考虑无解和多解的情况
//8.两个int连成爆long long的一定要加1ll！！！！
//9.先除后乘！！！！！！
template<class T>void read(T &x)
{
    x=0;int f=0;char ch=getchar();
    while(!isdigit(ch)){f|=(ch=='-');ch=getchar();}
    while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
    x=f?-x:x;
    return;
}
int t,n;
char s[maxn];
int z[maxn],sub[maxn],pre;
int cnt[27],num[27];
long long ans,sum[27];
int main()
{
    scanf("%d",&t);
    while(t--)
    {
        ans=0;
        scanf("%s",s+1);
        n=strlen(s+1);
        sub[n+1]=0;
        memset(num,0,sizeof(num));
        for(int i=n;i>=1;i--)
        {
            int c=s[i]-'a'+1;
            num[c]++;
            if(num[c]&1)
                sub[i]=sub[i+1]+1;
            else
                sub[i]=sub[i+1]-1;
        }
        memset(num,0,sizeof(num));
        memset(cnt,0,sizeof(cnt));
        memset(z,0,sizeof(z));
        pre=1;
        num[s[1]-'a'+1]=1;
        for(int i=2,l=1,r=0;i<=n;i++)
        {
            if(i<=r)
                z[i]=min(r-i+1,z[i-l+1]);
            while(i+z[i]<=n&&s[z[i]+1]==s[i+z[i]])
                z[i]++;
            if(i+z[i]-1>r)
            {
                l=i;
                r=i+z[i]-1;
            }
            if(i>2)
            {
                sum[0]=cnt[0];
                for(int j=1;j<=26;j++)
                    sum[j]=sum[j-1]+cnt[j];
                for(int j=1;j<=(min(n-1,i+z[i]-1)/(i-1));j++)
                    ans+=sum[sub[(i-1)*j+1]];
            }
            cnt[pre]++;
            int c=s[i]-'a'+1;
            num[c]++;
            if(num[c]&1)
                pre++;
            else
                pre--;
        }
        printf("%lld\n",ans);
    }
    return 0;
}

T3 移球游戏

解析：CCF 居然考构造了，居然还用了 SPJ，爷青结。

我在考场上的做法只能拿 $40$ pts。我想了一个基本操作，即交换任意两个球，但不改变其他球的位置，这样最后就像冒泡排序一样直接交换就行了，复杂度约为 $O(n ^{2}m ^{3})$ ，正好能够过前 $40$ 分的数据，并且步数和复杂度差不多。

怎么实现这个基本操作？我们假设两个球的位置为 $(i,j)$ 和 $(k,l)$ ， $(x,y)$ 代表第 $x$ 号柱子从下往上数第 $y$ 个球。我们先找到两个球中纵坐标更小，即深度更深的那个球，不妨设那个球就是 $(i,j)$ ，那么首先我们将第 $i$ 号柱的纵坐标为 $j\sim m$ 的球，即 $(i,j)$ 上面的所有球(包括它自己)，全部移动到空柱上，然后将第 $k$ 号柱纵坐标为 $l\sim m$ 的球，即在 $(k,l)$ 上面的球(包括它本身)，移动到第 $i$ 号柱上。然后此时将空柱子最上面的那个球，即 $(i,j)$ 移动到第 $k$ 号柱上，这时候第一个球就已经到达目标点了，再将 $i$ 号柱最上面那个球，即 $(k,l)$ 移动到空柱上，再把 $i$ 号柱上刚才由 $k$ 号柱转移过来的球放回 $k$ 号柱，这样 $k$ 号柱就只有 $(k,l)$ 变成了 $(i,j)$ ，最后再把空柱上所有的球放回 $i$ 号柱，交换就完成了。

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#define INF 1e9
using namespace std;
const int maxn=53,maxm=405,maxp=820000;
int n,m;
int a[maxn][maxm];
int ans[maxp<<2][2],cnt,ansp[maxp<<1][2],tot;
void move(int x,int y,int xx,int yy)
{
	if(y>yy)
	{
		swap(x,xx);
		swap(y,yy);
	}
	for(int i=m;i>=y;i--)
	{
		ans[++cnt][0]=x;
		ans[cnt][1]=n+1;
	}
	int top=m-y+1;
	for(int i=m;i>=yy;i--)
	{
		ans[++cnt][0]=xx;
		ans[cnt][1]=x;
	}
	ans[++cnt][0]=n+1;
	ans[cnt][1]=xx;
	ans[++cnt][0]=x;
	ans[cnt][1]=n+1;
	for(int i=m;i>=yy+1;i--)
	{
		ans[++cnt][0]=x;
		ans[cnt][1]=xx;
	}		
	for(int i=top;i>=1;i--)
	{
		ans[++cnt][0]=n+1;
		ans[cnt][1]=x;
	}
}
int main()
{
	//freopen("ball.in","r",stdin);
	//freopen("ball.out","w",stdout);
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			scanf("%d",&a[i][j]);
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
			if(a[i][j]!=i)
			{
				for(int k=i+1;k<=n;k++)
				{
					bool flag=0;
					for(int l=m;l>=1;l--)
						if(a[k][l]==i)
						{
							swap(a[i][j],a[k][l]);
							move(i,j,k,l);
							flag=1;
							break;
						}
					if(flag)
						break;
				}
			}
	}
	int now=1;
	while(now<=cnt)
	{
		while(ans[now][0]==ans[now+1][1]&&ans[now][1]==ans[now+1][0])
			now+=2;
		ansp[++tot][0]=ans[now][0];
		ansp[tot][1]=ans[now][1];
		now++;
	}
	printf("%d\n",tot);
	for(int i=1;i<=tot;i++)
		printf("%d %d\n",ansp[i][0],ansp[i][1]);
	return 0;
}

正解则是神奇的构造，给大佬跪了Orz。。。

NOIP2020 移球游戏解析

/*
 * @Author: clorf 
 * @Date: 2020-12-28 23:48:54 
 * @Last Modified by: clorf
 * @Last Modified time: 2020-12-29 01:13:03
 */
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<ctime>
#include<cctype>
#define INF 2e9
using namespace std;
const int maxn=55,maxm=405,maxl=820005;
const double Pi=acos(-1.0);
const double eps=1e-7;
//1.数组开小
//2.没用long long/爆了类型存储范围
//3.写之前式子没推清楚
//4.变量写错(想当然typo/没想清楚含义)
//5.写之前没想清楚复杂度
//6.常量数字与long long连用时要加ll！！！
//7.考虑无解和多解的情况
//8.两个int连成爆long long的一定要加1ll！！！！
//9.先除后乘！！！！！！
template<class T>void read(T &x)
{
	x=0;int f=0;char ch=getchar();
	while(!isdigit(ch)){f|=(ch=='-');ch=getchar();}
	while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
	x=f?-x:x;
	return;
}
int n,m,tot,ans[maxl][2];
int a[maxn][maxm],cnt[maxn],id[maxn];
inline void move(int x,int y)
{
	ans[++tot][0]=x;
	ans[tot][1]=y;
	a[y][++cnt[y]]=a[x][cnt[x]--];
}
inline int calc(int x,int y)
{
	int sum=0;
	for(int i=1;i<=m;i++)
		sum+=(a[x][i]==y);
	return sum;
}
inline int top(int x)
{
	return a[x][cnt[x]];
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
	{
		cnt[i]=m;
		id[i]=i;
		for(int j=1;j<=m;j++)
			scanf("%d",&a[i][j]);
	}
	cnt[n+1]=0;
	id[n+1]=n+1;
	for(int col=n;col>=3;col--)
	{
		int num=calc(id[1],col);
		for(int i=1;i<=num;i++)
			move(id[col],id[col+1]);
		for(int i=1;i<=m;i++)
		{
			if(top(id[1])==col)
				move(id[1],id[col]);
			else
				move(id[1],id[col+1]);
		}
		for(int i=1;i<=m-num;i++)
			move(id[col+1],id[1]);
		for(int i=1;i<=m;i++)
		{
			if(top(id[2])==col||cnt[id[1]]==m)
				move(id[2],id[col+1]);
			else
				move(id[2],id[1]);
		}
		swap(id[2],id[col+1]);
		swap(id[1],id[col]);
		for(int i=1;i<col;i++)
		{
			num=calc(id[i],col);
			for(int j=1;j<=num;j++)
				move(id[col],id[col+1]);
			for(int j=1;j<=m;j++)
			{
				if(top(id[i])==col)
					move(id[i],id[col]);
				else
					move(id[i],id[col+1]);
			}
			swap(id[i],id[col+1]);
			swap(id[i],id[col]);
		}
		for(int i=1;i<col;i++)
			while(top(id[i])==col)
				move(id[i],id[col+1]);
		for(int i=1;i<col;i++)
			while(cnt[id[i]]<m)
				move(id[col],id[i]);
	}
	int num=calc(id[1],1);
	for(int i=1;i<=num;i++)
		move(id[2],id[3]);
	for(int i=1;i<=m;i++)
	{
		if(top(id[1])==1)
			move(id[1],id[2]);
		else
			move(id[1],id[3]);
	}
	for(int i=1;i<=num;i++)
		move(id[2],id[1]);
	for(int i=1;i<=m-num;i++)
		move(id[3],id[1]);
	while(cnt[id[3]])
		move(id[3],id[2]);
	for(int i=1;i<=m-num;i++)
		move(id[1],id[3]);
	for(int i=1;i<=m;i++)
	{
		if(top(id[2])==1)
			move(id[2],id[1]);
		else
			move(id[2],id[3]);
	}
	printf("%d\n",tot);
	for(int i=1;i<=tot;i++)
		printf("%d %d\n",ans[i][0],ans[i][1]);
	return 0;
}

T4 微信步数

解析：一道难难难题，但是还是套路题(虽然我不会)。

我们考虑所有点一起走。设 $p _{i,j}$ 是走完第 $i$ 步后第 $j$ 维的变化量(可正可负)，根据它的定义，可得 $\displaystyle{p _{i,j}=\sum _{1\le k\le i,c _{(k-1)\bmod n+1}=j}}d _{(k-1)\bmod n+1}$ 。再定义从开始到走完第 $i$ 步的过程中，第 $j$ 维的变化量的最大最小值分别为 $maxx _{i,j},minn _{i,j}$ ，即是 $p$ 数组的前缀最大最小值。

可以发现，初始位置第 $j$ 维范围在 $[1,-minn _{i,j}]\bigcup [w _{j}-maxx _{i,j}+1,w _{j}]$ 的这些位置到走完第 $i$ 步的时候都已经超出边界，不再走了。我们令 $l _{i,j}=-minn _{i,j}+1,r _{i,j}=w _{j}-maxx _{i,j}$ ，那么到第 $i$ 步时，第 $j$ 维可以存活的位置个数为 $r _{i,j}-l _{i,j}+1=w _{j}-maxx _{i,j}+minn _{i,j}$ ，同时可得对于任意一个起点 $(a _{1},a _{2},\cdots,a _{k})$ 走了 $i$ 步还存活，即没有超出边界的充要条件是它的任意一维都有 $a _{j}\in [l _{i,j},r _{i,j}]$ ，那么总共存活的起点数量即为 $\displaystyle{\prod _{j=1} ^{k}(r _{i,j}-l _{i,j}+1)}$ 。

我们定义所有起点中最长不超出边界的移动时间，即最长存活时间为 $\text{T}$ 步(当然如果存在永远走不出去的说明走完一轮 $n$ 步后这一维的偏移量为 $0$ ，一开始就可以判断然后输出 $-1$ 即可)，那么答案即为 $\displaystyle{\sum _{i=0} ^{\text{T}}\prod _{j=1} ^{k}(r _{i,j}-l _{i,j}+1)}$ ，其中 $l _{i,j},r _{i,j}$ 可以在循环中很方便计算，由于 $\text{T}$ 在非 $-1$ 情况下最大为 $n\times \max(w _{i})$ (即某一维一轮偏移量最小为 $1$ ，那么某个端点就要走 $w _{i}\times n$ 步，所以总共最大步数即为 $n\times \max(w _{i})$ )，这样我们得到了一个 $O(nk\max(w _{i}))$ 的做法，可以通过 $45$ pts 的点。(~~但是打暴力就有 $35$ pts！！！再算上 $k=1$ 的情况就 $45$ 了！！！~~)

考虑优化这个算法。经过手玩或者画图可以发现一个结论：

任意一维从第一轮(一轮指走 $n$ 步)后，每一轮死掉的点数是一样的，即从第二轮开始每一轮死掉的点一样。

为啥呢？

我们手推一下，首先走完第一轮过程中死掉的第 $j$ 维起点坐标为 $a _{j}=maxx _{n,j}-minn _{n,j}$ ，这个可以用我们前面算法的结论，由于走完第 $n$ 步活着的位置只有 $w _{j}-maxx _{n,j}+minn _{n,j}$ 个，所以死了的有 $maxx _{n,j}-minn _{n,j}$ 个。第二轮以及以后的每一轮过程中，死掉的起点坐标数量为 $b _{j}=maxx _{2n,j}-minn _{2n,j}-a _{j}$ ，即前两轮死去的点数减去第一轮死去的点数。接下来我们证明这个性质。

我们对于第 $j$ 维，画出以步数 $i$ 作为横坐标， $p _{i,j}$ 作为纵坐标的一个图像，容易发现这是一个类似这样的折线图：

折线图

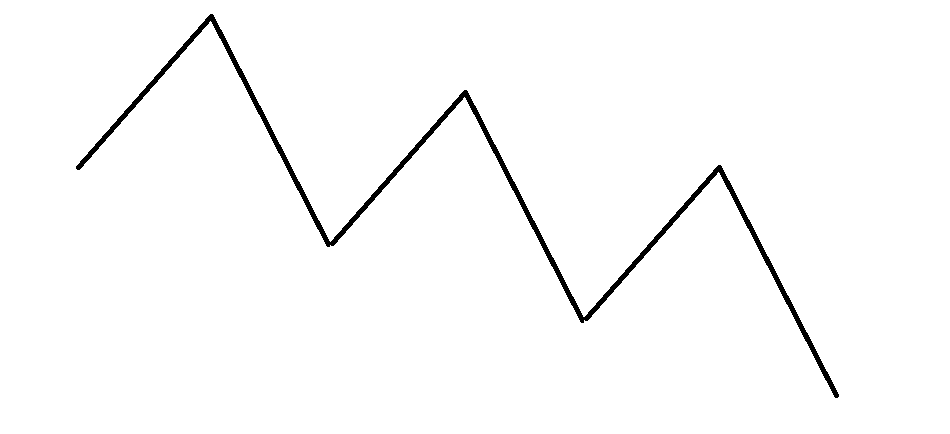
它具有长度为 $n$ 的周期，正好一轮，第一轮死掉的人数根据公式可得是第二根斜线的纵坐标相差值，而后来由于 $maxx$ 一直不变(也可能是 $minn$ ，但肯定有一个极值不变)，另一个极值每个周期，即每轮规律性下降一样的纵坐标，而 $a _{j}$ 是定值，因此后来的每一轮死去的人数样。

然后我们就可以开始推式子啦！！

首先

r _{i,j}-l _{i,j}+1=\begin{cases} w _{j}-(maxx _{i,j}-minn _{i,j}) & i\le n\\ w _{j}-a _{j}-\left\lfloor\dfrac{i-n}{n}\right\rfloor\times b _{j}-f _{i\bmod n,j} & i>n \end{cases}

其中我们令 $f _{i,j}=(maxx _{i+n,j}-minn _{i+n,j})-a _{j}~(0\le i\le n-1)$ 。

然后推答案式子

\begin{aligned} ans & = \sum _{i=0} ^{\text{T}}\prod _{j=1} ^{k}(r _{i,j}-l _{i,j}+1)\\ & =\sum _{i=0} ^{n-1}\prod _{j=1} ^{k}[w _{j}-(maxx _{i,j}-minn(i,j))]+\sum _{i=n} ^{\text{T}}\prod _{j=1} ^{k}(w _{j}-a _{j}-\left\lfloor\dfrac{i-n}{n}\right\rfloor\times b _{j}-f _{i\bmod n,j}) \end{aligned}

即分为 $i\le n,i>n$ 的两部分统计答案，其中第一部分，即第一个和式可以直接 $O(nk)$ 枚举算出，接下来继续推第二个和式

\begin{aligned} & \sum _{i=n} ^{\text{T}}\prod _{j=1} ^{k}(w _{j}-a _{j}-\left\lfloor\dfrac{i-n}{n}\right\rfloor\times b _{j}-f _{i\bmod n,j})\\ = & \sum _{i=0} ^{n-1}\sum _{x=0} ^{\lfloor\frac{\text{T}-n-i}{n}\rfloor}\prod _{j=1} ^{k}(w _{j}-a _{j}-x\times b _{j}-f _{i,j}) \end{aligned}

即枚举 $i\bmod n$ 的余数，和 $b _{j}$ 的系数，可以发现后面的连乘号展开后是一个关于 $x$ 的 $k$ 次多项式，即 $\sum _{j=0} ^{k}e _{i,j}x ^{j}$ ，我们可以 $O(nk ^{2})$ 算出 $e _{i,j}$ ，然后继续化简

\begin{aligned} & \sum _{i=0} ^{n-1}\sum _{x=0}^{\lfloor\frac{\text{T}-n-i}{n}\rfloor}\sum _{j=0} ^{k}e _{i,j}x ^{j}\\ = & \sum _{i=0} ^{n-1}\sum _{j=0} ^{k}e _{i,j}\sum _{x=0} ^{\lfloor\frac{\text{T}-n-i}{n}\rfloor}x ^{j} \end{aligned}

可以发现最后一部分是自然数幂和，其实可以插值处理。但由于本题 $k\le 10$ ，对于 $k\le 3$ 的时候我们可以直接用平方和立方和的公式， $k>3$ 的时候由于 $\dfrac{\text{T}}{n}=\max(w _{i})$ 最大也只有 $10 ^{6}$ ，我们直接暴力预处理就好。

关于 $\text{T}$ 的计算，即所有维活着的人数都开始为 $0$ ，根据第二个和式括号里的公式，直接 $O(nk)$ 枚举算出它为 $0$ 的时候的步数，对所有维的这个值取 $\min$ 即可。

/*
 * @Author: clorf 
 * @Date: 2021-01-02 09:39:45 
 * @Last Modified by: clorf
 * @Last Modified time: 2021-01-02 11:29:54
 */
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<ctime>
#include<cctype>
#define INF 1e18
#define int long long
using namespace std;
const int maxn=500010,maxk=12;
const int mod=1e9+7;
const double Pi=acos(-1.0);
const double eps=1e-7;
//1.数组开小
//2.没用long long/爆了类型存储范围
//3.写之前式子没推清楚
//4.变量写错(想当然typo/没想清楚含义)
//5.写之前没想清楚复杂度
//6.常量数字与long long连用时要加ll！！！
//7.考虑无解和多解的情况
//8.两个int连成爆long long的一定要加1ll！！！！
//9.先除后乘！！！！！！
template<class T>void read(T &x)
{
	x=0;int f=0;char ch=getchar();
	while(!isdigit(ch)){f|=(ch=='-');ch=getchar();}
	while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
	x=f?-x:x;
	return;
}
int n,k;
int c[maxn],d[maxn];
long long w[maxk],pre[maxk];
long long maxx[maxn<<1][maxk],minn[maxn<<1][maxk];
long long f[maxn][maxk],ans,inv2,inv6,e[maxn][maxk];
long long sum[maxn<<1][maxk],a[maxk],b[maxk],all;
inline long long inc(long long x,long long y)
{
	return x+y>=mod?x+y-mod:x+y;
}
inline long long getnum(long long n,long long k)
{
	long long num=(n+1)*n%mod*inv2%mod;
	if(!k)
		return n+1;
	if(k==1)
		return num;
	if(k==2)
		return (n+1)*n%mod*(2*n+1)%mod*inv6%mod;
	if(k==3)
		return num*num%mod;
	return sum[n][k]%mod;
}
inline long long power(long long a,long long b,long long p)
{
	long long ans=1;
	for(;b;b>>=1)
	{
		if(b&1)
			ans=ans*a%p;
		a=a*a%p;
	}
	return ans%p;
}
signed main()
{
	inv2=power(2ll,mod-2,mod);
	inv6=power(6ll,mod-2,mod);
	for(int i=1;i<=(maxn<<1)-1;i++)
	{
		long long x=i*i%mod*i*i%mod;
		for(int j=4;j<=10;j++)
		{
			sum[i][j]=inc(sum[i-1][j],x);
			x=x*i%mod;
		}
	}
	read(n);
	read(k);
	for(int i=1;i<=k;i++)
		read(w[i]);
	for(int i=1;i<=n;i++)
	{
		read(c[i]);
		read(d[i]);
		for(int j=1;j<=k;j++)
		{
			maxx[i][j]=maxx[i-1][j];
			minn[i][j]=minn[i-1][j];
		}
		pre[c[i]]+=d[i];
		maxx[i][c[i]]=max(maxx[i][c[i]],pre[c[i]]);
		minn[i][c[i]]=min(minn[i][c[i]],pre[c[i]]);
	}
	bool flag=0;
	for(int i=1;i<=k;i++)
		if(pre[i]||maxx[n][i]-minn[n][i]>=w[i])
		{
			flag=1;
			break;
		}
	if(!flag)
	{
		printf("-1");
		return 0;
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=k;j++)
		{
			maxx[i+n][j]=maxx[i+n-1][j];
			minn[i+n][j]=minn[i+n-1][j];
		}
		pre[c[i]]+=d[i];
		maxx[i+n][c[i]]=max(maxx[i+n][c[i]],pre[c[i]]);
		minn[i+n][c[i]]=min(minn[i+n][c[i]],pre[c[i]]);
	}
	for(int j=1;j<=k;j++)
	{
		a[j]=maxx[n][j]-minn[n][j];
		b[j]=maxx[n<<1][j]-minn[n<<1][j]-a[j];
		for(int i=0;i<n;i++)
			f[i][j]=maxx[i+n][j]-minn[i+n][j]-a[j];
	}
	flag=1;
	for(int i=0;i<n;i++)
	{
		long long num=1;
		for(int j=1;j<=k;j++)
		{
			if(w[j]<=maxx[i][j]-minn[i][j])
				flag=0;
			else
				num=num*(w[j]-maxx[i][j]+minn[i][j])%mod;
		}
		if(flag)
			ans=inc(ans,num);
	}
	if(!flag)
	{
		printf("%lld",ans);
		return 0;
	}
	all=INF;
	for(int i=1;i<=k;i++)
	{
		if(!b[i])
			continue;
		long long m=(w[i]-a[i]-1)/b[i]*n;
		for(int j=0;j<n;j++)
			if(w[i]-a[i]-(m/n)*b[i]-f[j][i]==0)
			{
				all=min(1ll*(m+n+j-1),all);
				break;
			}
	} 
	for(int i=0;i<n;i++)
	{
		if(all<n+i)
			break;
		e[i][0]=1ll;
		for(int j=1;j<=k;j++)
			for(int l=k;l>=0;l--)
				e[i][l]=inc((l?e[i][l-1]*(mod-b[j])%mod:0ll),e[i][l]*(w[j]-a[j]-f[i][j])%mod);
		for(int j=0;j<=k;j++)
			ans=inc(ans,e[i][j]*getnum((all-i)/n-1,j)%mod);
	}
	ans=(ans+mod)%mod;
	printf("%lld",ans);
	return 0;
}