最小生成树是图论的最基础算法之一,使用广泛,这篇文章主要总结最小生成树的套路。
最小生成树一般有 Kruskal 和 Prim 两种算法,第一种算法复杂度为 ,采用并查集实现,适合稀疏图,代码很好实现;第算法复杂度为 ,跟 Dijkstra 算法有异曲同工之妙,适合稠密图,代码要较难一点。此外,还有第三种算法 Boruvka,复杂度为 ,是前两种算法的结合,有兴趣的可以自己查阅资料 Boruvka 算法。
关于 Kruskal 算法,可以引申出一个新的数据结构——Kruskal 重构树。我们在运行 Kruskal 算法的同时,对于两个可以合并的节点 ,新建一个节点 ,把 向 连边作为它们的父亲,同时把 的点权设为 的边权,最后就会生成一棵 个节点的树,即 Kruskal 重构树。Kruskal 重构树有许多有意思的性质。首先根据构造过程,这是一个二叉堆(如果 Kruskal 最小生成树构造则是大根堆,最大生成树则是小根堆);其次,两点之间的边权最大值是 Kruskal 树上它们 LCA 的点权;最后,只有 Kruskal 重构树的 个叶子节点是原图的节点,其他 个节点则是最小生成树上的每一条边。
例 1
瓶颈生成树&最小瓶颈路。
解析:首先最小生成树是瓶颈生成树的充分不必要条件。即最小生成树一定是瓶颈生成树,而瓶颈生成树不一定是最小生成树。所以对于两点之间的最小瓶颈路,那么一定是两点在最小生成树上路径的最大边权。接着就是求两个点在最小生成树上路径的最大边权。我们可以通过建 Kruskal 重构树将其转化为求 Kruskal 重构树上两点 LCA 的点权。注意这题的加强版求 LCA 用倍增算法为 TLE,因此用 tarjan LCA 或 欧拉序+ST表 求 LCA 即可。
/*
* @Author: clorf
* @Date: 2020-08-28 20:56:36
* @Last Modified by: clorf
* @Last Modified time: 2020-08-28 21:11:50
*/
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<ctime>
#include<vector>
#define INF 1e9
#pragma GCC optimize(2)
using namespace std;
const int maxn=500010,maxm=500101;
const int mod=1000000007;
const double Pi=acos(-1.0);
template<class T>inline void read(T &x)
{
x=0;int f=0;char ch=getchar();
while(ch<'0'||ch>'9') {ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return;
}
long long n,m,Q,tot;
long long A,B,C,P,val[maxn];
long long fa[maxn],dep[maxn],sum;
long long head[maxn],cnt,col[maxn];
vector<long long> q[maxn];
struct node
{
long long next;
long long to;
long long num;
}e[maxm<<1];
struct edge
{
long long x;
long long y;
long long z;
}s[maxm<<1];
inline void add(long long from,long long to,long long num)
{
e[++cnt].next=head[from];
e[cnt].to=to;
e[cnt].num=num;
head[from]=cnt;
}
inline bool cmp(edge a,edge b)
{
return a.z<b.z;
}
inline long long rnd()
{
return A=(A*B+C)%P;
}
long long getfa(long long x)
{
if(fa[x]==x)
return x;
return fa[x]=getfa(fa[x]);
}
void dfs(long long u)
{
//printf("%d\n",u);
col[u]=1;
for(int i=head[u];i;i=e[i].next)
{
int v=e[i].to;
if(col[v])
continue;
dfs(v);
fa[v]=u;
}
int l=q[u].size();
for(int i=0;i<l;i++)
{
int v=q[u][i];
if(col[v]==2)
{
int lca=getfa(v);
//printf("%d %d %d %d\n",u,v,lca,val[lca]);
sum=(sum%mod+val[lca]%mod)%mod;
}
}
col[u]=2;
}
int main()
{
scanf("%lld%lld",&n,&m);
tot=n;
for(int i=1;i<=m;i++)
scanf("%lld%lld%lld",&s[i].x,&s[i].y,&s[i].z);
sort(s+1,s+m+1,cmp);
for(int i=1;i<=2*n;i++)
fa[i]=i;
for(int i=1;i<=m;i++)
{
int x=getfa(s[i].x);
int y=getfa(s[i].y);
if(x!=y)
{
val[++tot]=s[i].z;
fa[x]=fa[y]=fa[tot]=tot;
add(tot,x,0);
add(tot,y,0);
}
if(tot==2*n-1)
break;
}
scanf("%lld",&Q);
scanf("%lld%lld%lld%lld",&A,&B,&C,&P);
for(int i=1;i<=Q;i++)
{
long long u=rnd()%n+1;
long long v=rnd()%n+1;
q[u].push_back(v);
q[v].push_back(u);
}
for(int i=1;i<=2*n;i++)
fa[i]=i;
dfs(tot);
printf("%lld\n",sum);
return 0;
}例 2
切比雪夫最小生成树。
解析:首先了解两点 间的切比雪夫距离为 。对于两个点 ,我们建立两条边,长度分别为 (建立两条边是把切比雪夫距离中取 的操作交给了 Kruskal 算法来做)。接着对于三个点 ,其中 ,那么由于 ,所以 这条边不需要建。对于纵坐标同理。因此我们只要对 个点分别按照横纵坐标排序,将相邻两个点及横纵坐标差的绝对值当作一条边加进去,最后把这 条边跑 Kruskal 算法即可。
/*
* @Author: clorf
* @Date: 2020-08-29 17:07:51
* @Last Modified by: clorf
* @Last Modified time: 2020-08-29 17:31:41
*/
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<ctime>
#define INF 1e9
using namespace std;
const int maxn=100010;
const double Pi=acos(-1.0);
template<class T>void read(T &x)
{
x=0;int f=0;char ch=getchar();
while(ch<'0'||ch>'9') {f|=(ch=='-');ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return;
}
int n,ans,fa[maxn],cnt;
struct city
{
int x;
int y;
int id;
}e[maxn];
struct edge
{
int x;
int y;
int z;
}s[maxn];
bool cmp(edge a,edge b)
{
return a.z<b.z;
}
inline int dis(int a,int b,int c,int d)
{
return min(abs(a-c),abs(b-d));
}
inline bool cmp1(city a,city b)
{
return a.x<b.x;
}
inline bool cmp2(city a,city b)
{
return a.y<b.y;
}
int getfa(int x)
{
if(fa[x]==x)
return x;
return fa[x]=getfa(fa[x]);
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d%d",&e[i].x,&e[i].y);
e[i].id=i;
}
for(int i=1;i<=n;i++)
fa[i]=i;
sort(e+1,e+n+1,cmp1);
for(int i=2;i<=n;i++)
s[++cnt]=(edge){e[i].id,e[i-1].id,abs(e[i].x-e[i-1].x)};
sort(e+1,e+n+1,cmp2);
for(int i=2;i<=n;i++)
s[++cnt]=(edge){e[i].id,e[i-1].id,abs(e[i].y-e[i-1].y)};
sort(s+1,s+cnt+1,cmp);
for(int i=1;i<=cnt;i++)
{
int x=getfa(s[i].x);
int y=getfa(s[i].y);
if(x!=y)
{
fa[x]=y;
ans+=s[i].z;
}
}
printf("%d",ans);
return 0;
}例 3
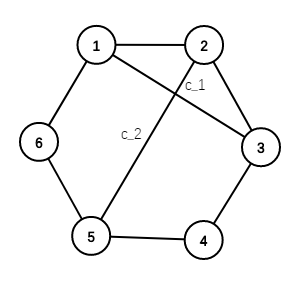
个点排成一个环,给出 个三元组 ,对每个三元组建边 ,求最小生成树。
解析:这道题要搞清楚最小生成树算法的本质才能做出来。这道题需要用到 Prim 算法的思想,即我们每次都是选未在目前最小生成树结点集合的一个点和在目前最小生成树节点集合的一个点的最小的边相连接,简而言之就是选连接两个连通块最小的边,然后把边上的点从第二个连通块删除加入第一个连通块。对于这道题,我们发现每个三元组的建边方式很奇特,它保证一个三元组在其建边过程中,一直只有一个连通块。每次加边都是把不在连通块上的点与连通块连边。因此,我们可以借助这一点性质,反正都是往连通块上连边,所以我们不需要在意连连通块上的哪一个点。
比如最开始是这样连边:
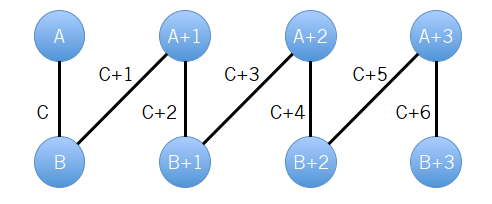
我们可以依次做出以下改变:
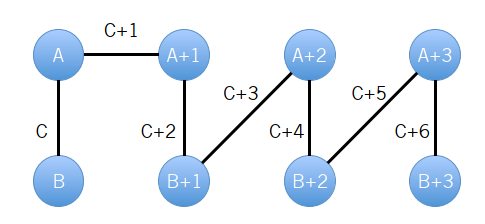

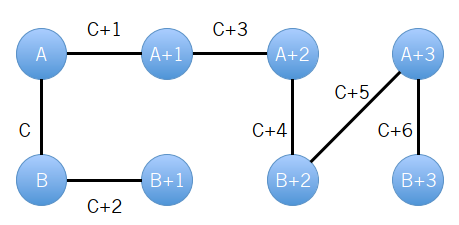
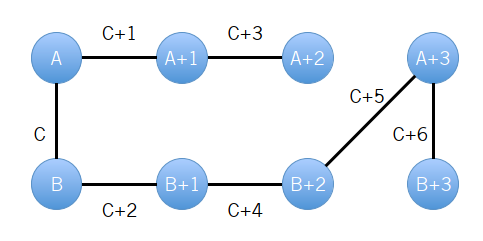
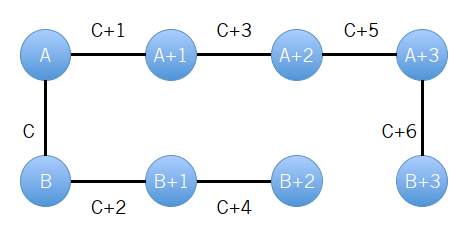
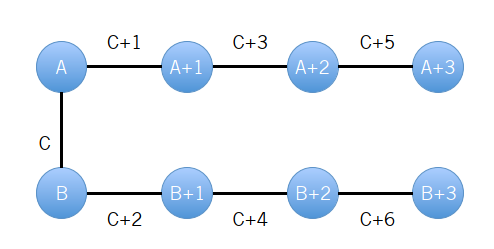
即我们把所有在环内的边改成了绕环的边,并且从 和 出发的边权依次增加 。因此我们最后就会变成如下形式:
即除了每个初始三元组的边在环内,其他的边都可改为绕环的边。
发现绕环的每条边可能会被很多个三元组更新,我们需要取最小值,由于每个三元组边权的单调性,因此每条边最多只会被同一个三元组更新一次,绕着环跑两圈(第一次找到最小的三元组,第二次才能用最小的更新整个环上的边),每次更新边权和此时的三元组即可。最后把更新完后的绕环的 条边,和 个三元组的初始边一起跑 Kruskal 算法即可。
/*
* @Author: clorf
* @Date: 2020-08-31 20:27:12
* @Last Modified by: clorf
* @Last Modified time: 2020-08-31 21:35:03
*/
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<ctime>
#define INF 1e9
using namespace std;
const int maxn=200010;
const double Pi=acos(-1.0);
template<class T>void read(T &x)
{
x=0;int f=0;char ch=getchar();
while(ch<'0'||ch>'9') {f|=(ch=='-');ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return;
}
int n,q,cnt;
int fa[maxn];
long long p[maxn],ans;
struct edge
{
int x;
int y;
long long z;
}s[maxn],e[maxn<<1];
inline bool cmp(edge a,edge b)
{
return a.z<b.z;
}
inline int sub(int x)
{
return (x+1)%n;
}
int getfa(int x)
{
if(fa[x]==x)
return x;
return fa[x]=getfa(fa[x]);
}
int main()
{
memset(p,0x3f,sizeof(p));
scanf("%d%d",&n,&q);
for(int i=1;i<=q;i++)
{
scanf("%d%d%lld",&s[i].x,&s[i].y,&s[i].z);
e[++cnt]=(edge){s[i].x,s[i].y,s[i].z};
p[s[i].x]=min(p[s[i].x],s[i].z+1);
p[s[i].y]=min(p[s[i].y],s[i].z+2);
}
int now=s[1].x,tot=2*n;
long long sum=p[now];
while(tot--)
{
if(sum<p[now])
p[now]=sum;
else
sum=p[now];
sum+=2;
now=sub(now);
}
for(int i=0;i<n;i++)
e[++cnt]=(edge){i,sub(i),p[i]};
for(int i=0;i<=n;i++)
fa[i]=i;
sort(e+1,e+cnt+1,cmp);
for(int i=1;i<=cnt;i++)
{
int x=getfa(e[i].x);
int y=getfa(e[i].y);
if(x!=y)
{
fa[x]=y;
ans+=e[i].z;
}
}
printf("%lld",ans);
return 0;
}
例 4
解析:我们需要从连通块的角度切入,易知要打通一个连通块的花费为 。首先判断先加哪条边构成连通块。容易证明先加边权小的比先加边权大的更优。考虑链上三个点 。那么先连 再连 是比只连 更优的。先连 再连 的花费为 ,而只连 的花费是 。这说明如果我们要连一条边时,那么同时也要把比它小的边全都连上,所以我们需要从小到大连边。因此我们只需要在 Kruskal 的同时维护答案 ,对于连通块 和 ,若我们不连这条边,那么答案就为 ,否则连边答案就为 ,同时维护连通块的最大 值和最小 值。
/*
* @Author: clorf
* @Date: 2020-08-31 21:39:59
* @Last Modified by: clorf
* @Last Modified time: 2020-08-31 22:44:02
*/
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<ctime>
#define INF 1e9
using namespace std;
const int maxn=100010;
const double Pi=acos(-1.0);
template<class T>void read(T &x)
{
x=0;int f=0;char ch=getchar();
while(ch<'0'||ch>'9') {f|=(ch=='-');ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return;
}
int n,m,fa[maxn];
long long maxx[maxn],minn[maxn];
long long ans[maxn],num;
struct edge
{
int x;
int y;
long long z;
}e[maxn<<2];
inline bool cmp(edge a,edge b)
{
return a.z<b.z;
}
int getfa(int x)
{
if(fa[x]==x)
return x;
return fa[x]=getfa(fa[x]);
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
fa[i]=i;
scanf("%lld%lld",&maxx[i],&minn[i]);
ans[i]=maxx[i]*minn[i];
}
for(int i=1;i<=m;i++)
scanf("%d%d%lld",&e[i].x,&e[i].y,&e[i].z);
sort(e+1,e+m+1,cmp);
for(int i=1;i<=m;i++)
{
int x=getfa(e[i].x);
int y=getfa(e[i].y);
if(x!=y)
{
fa[x]=y; ans[y]=min(ans[x]+ans[y],max(e[i].z*min(minn[x],minn[y]),max(maxx[x],maxx[y])*min(minn[x],minn[y])));
maxx[y]=max(maxx[y],maxx[x]);
minn[y]=min(minn[y],minn[x]);
}
}
for(int i=1;i<=n;i++)
if(fa[i]==i)
num+=ans[i];
printf("%lld",num);
return 0;
}例 5
无向带权图,每条边都是黑色或白色。求恰好有 条白边的最小生成树。
解析:这是 wqs二分 的一道经典题目。我们把二分一个值,接着把白边的边权都加上这个值,接着跑 Kruskal(当边权相等时优先考虑白边),看看最小生成树的白边树是否大于等于 。由于白边加的这个值如果越大,那么选中的白边就相应越少,具有一个单调性,并且对于所有白边都会加上同一个值,不会影响白边加入的相对顺序,只会改变白边与黑边之间的顺序,因此可以二分。
/*
* @Author: clorf
* @Date: 2020-08-27 14:52:10
* @Last Modified by: clorf
* @Last Modified time: 2020-08-27 16:09:02
*/
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<ctime>
#define INF 1e9
using namespace std;
const int maxn=100010;
const double Pi=acos(-1.0);
template<class T>void read(T &x)
{
x=0;int f=0;char ch=getchar();
while(ch<'0'||ch>'9') {f|=(ch=='-');ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return;
}
struct edge
{
int x;
int y;
int z;
int col;
}s[maxn];
bool cmp(edge a,edge b)
{
if(a.z==b.z)
return a.col<b.col;
return a.z<b.z;
}
int n,m,need,maxx,k;
int fa[maxn],ans,sum;
int getfa(int x)
{
if(fa[x]==x)
return x;
return fa[x]=getfa(fa[x]);
}
bool check(int x)
{
for(int i=1;i<=m;i++)
if(!s[i].col)
s[i].z+=x;
for(int i=1;i<=n;i++)
fa[i]=i;
sum=k=0;
sort(s+1,s+m+1,cmp);
for(int i=1;i<=m;i++)
{
int a=getfa(s[i].x);
int b=getfa(s[i].y);
if(a==b)
continue;
else
{
fa[a]=b;
sum+=s[i].z;
k+=(s[i].col^1);
}
}
return k>=need;
}
void clean(int x)
{
for(int i=1;i<=m;i++)
if(!s[i].col)
s[i].z-=x;
}
int main()
{
scanf("%d%d%d",&n,&m,&need);
for(int i=1;i<=m;i++)
{
scanf("%d%d%d%d",&s[i].x,&s[i].y,&s[i].z,&s[i].col);
s[i].x++;
s[i].y++;
maxx=max(maxx,s[i].z);
}
int l=-INF,r=INF,mid;
while(l<r)
{
mid=(l+r)/2;
if(check(mid))
{
ans=sum-need*mid;
l=mid+1;
}
else
r=mid;
clean(mid);
}
printf("%d\n",ans);
return 0;
}例 6
最小生成树的必经边,非必经边和非最小生成树边判断。
解析:首先判断可以在最小生成树上的边,包括所有必经边和非必经边,那么它的补集就是非最小生成树边。对于可以在最小生成树上的边,我们可以排序后对于权值相等的边,加入任何一条都不会改变总的权值,因此我们统计权值相等的边中,端点不在同一个集合的数量即可。这样我们就可以算出非最小生成树边的数量。接着就是从可以在最小生成树上的边中找必经边,即每个最小生成树都会经过的边。可以删掉这条边后再跑一遍最小生成树,如果总权值增大了那它就是必经边。暴力算法是 的复杂度,但是可以借助预处理删掉某条树边后的最小生成树优化到 ,可以详细见这道题:BZOJ2238 Mst。
/*
* @Author: clorf
* @Date: 2020-09-01 16:33:17
* @Last Modified by: clorf
* @Last Modified time: 2020-09-01 21:21:21
*/
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<ctime>
#define INF 1e9
using namespace std;
const int maxn=100010;
const double Pi=acos(-1.0);
template<class T>void read(T &x)
{
x=0;int f=0;char ch=getchar();
while(ch<'0'||ch>'9') {f|=(ch=='-');ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return;
}
int t,n,m,fa[maxn],ans;
struct edge
{
int x;
int y;
int z;
}a[maxn];
int getfa(int x)
{
if(fa[x]==x)
return x;
return fa[x]=getfa(fa[x]);
}
bool cmp(edge a,edge b)
{
return a.z<b.z;
}
int main()
{
scanf("%d",&t);
while(t--)
{
int ans=0;
memset(a,0,sizeof(a));
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].z);
sort(a+1,a+m+1,cmp);
for(int i=1;i<=n;i++)
fa[i]=i;
int j;
for(int i=1;i<=m;i=j)
{
for(j=i;a[j].z==a[i].z;j++)
if(getfa(a[j].x)!=getfa(a[j].y))
ans++;
for(j=i;a[j].z==a[i].z;j++)
if(getfa(a[j].x)!=getfa(a[j].y))
fa[getfa(a[j].x)]=getfa(a[j].y);
}
printf("%d\n",ans);
}
return 0;
}例 7
最小生成树的唯一性。
解析:可以用上一题的结论。如果可以在最小生成树上的边只有 条,那么这个最小生成树就是唯一的。
/*
* @Author: clorf
* @Date: 2020-09-01 21:13:40
* @Last Modified by: clorf
* @Last Modified time: 2020-09-01 21:22:09
*/
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<ctime>
#define INF 1e9
using namespace std;
const int maxn=10010;
const double Pi=acos(-1.0);
template<class T>void read(T &x)
{
x=0;int f=0;char ch=getchar();
while(ch<'0'||ch>'9') {f|=(ch=='-');ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return;
}
int t,n,m,fa[maxn];
struct edge
{
int x;
int y;
int z;
}s[maxn];
inline bool cmp(edge a,edge b)
{
return a.z<b.z;
}
int getfa(int x)
{
if(fa[x]==x)
return x;
return fa[x]=getfa(fa[x]);
}
int main()
{
scanf("%d",&t);
while(t--)
{
memset(s,0,sizeof(s));
int ans=0,sum=0;
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
scanf("%d%d%d",&s[i].x,&s[i].y,&s[i].z);
for(int i=1;i<=n;i++)
fa[i]=i;
sort(s+1,s+m+1,cmp);
int j=1;
for(int i=1;i<=m;i=j)
{
for(j=i;s[j].z==s[i].z;j++)
if(getfa(s[j].x)!=getfa(s[j].y))
ans++;
for(j=i;s[j].z==s[i].z;j++)
if(getfa(s[j].x)!=getfa(s[j].y))
{
fa[getfa(s[j].x)]=getfa(s[j].y);
sum+=s[j].z;
}
}
if(ans==n-1)
printf("%d\n",sum);
else
printf("Not Unique!\n");
}
return 0;
}例 8
最小生成树计数。
解析:这题正解应该是要用到矩阵树(Matrix-Tree)定理,但由于我不会,于是只能暴搜。
首先最小生成树有一个特殊的性质,那就是所有的最小生成树权值相同的边的数量是一样的。我们首先求出任意一个最小生成树,然后如果加一条边,就必须在这个环上删一条边。如果删去的边比加入的边小,那么新的生成树就不是最小生成树了;如果相反,那么最开始的最小生成树就不是最小生成树了。因此只有删去的边和加入的边权值相等,才能保证两棵树都是最小生成树。因此我们暴力搜索,判断在权值相同的边中有多少种方式能不成环,最后用乘法原理就行了。需要注意的是并查集不能路径压缩,因为我们暴搜需要回溯。
/*
* @Author: clorf
* @Date: 2020-08-27 17:48:08
* @Last Modified by: clorf
* @Last Modified time: 2020-08-27 20:31:37
*/
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<ctime>
#define INF 1e9
using namespace std;
const int maxn=1010;
const int mod=31011;
const double Pi=acos(-1.0);
template<class T>void read(T &x)
{
x=0;int f=0;char ch=getchar();
while(ch<'0'||ch>'9') {f|=(ch=='-');ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return;
}
int n,m,fa[maxn],sum;
int cnt,tot,ans=1;
struct edge
{
int x;
int y;
int z;
}e[maxn<<1];
bool cmp(edge a,edge b)
{
return a.z<b.z;
}
struct array
{
int l;
int r;
int num;
}s[maxn];
int getfa(int x)
{
if(fa[x]==x)
return x;
return getfa(fa[x]);
}
void dfs(int i,int q,int now)
{
if(now==s[i].r+1)
{
if(q==s[i].num)
sum++;
return ;
}
int x=getfa(e[now].x);
int y=getfa(e[now].y);
if(x!=y)
{
fa[x]=y;
dfs(i,q+1,now+1);
fa[x]=x;
fa[y]=y;
}
dfs(i,q,now+1);
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
scanf("%d%d%d",&e[i].x,&e[i].y,&e[i].z);
sort(e+1,e+m+1,cmp);
for(int i=1;i<=n;i++)
fa[i]=i;
for(int i=1;i<=m;i++)
{
if(e[i].z!=e[i-1].z)
{
s[cnt].r=i-1;
s[++cnt].l=i;
}
int x=getfa(e[i].x);
int y=getfa(e[i].y);
if(x!=y)
{
s[cnt].num++;
fa[x]=y;
tot++;
}
}
s[cnt].r=m;
if(tot!=n-1)
{
printf("0");
return 0;
}
for(int i=1;i<=n;i++)
fa[i]=i;
for(int i=1;i<=cnt;i++)
{
sum=0;
dfs(i,0,s[i].l);
//printf("%d\n",sum);
ans=ans*sum%mod;
for(int j=s[i].l;j<=s[i].r;j++)
{
int x=getfa(e[j].x);
int y=getfa(e[j].y);
if(x!=y)
fa[x]=y;
}
}
printf("%d",ans);
return 0;
}例 9
严格次小生成树或非严格次小生成树。
解析:首先考虑非严格次小生成树。我们求次小生成树,是将非树边加入进去,再在环上删掉一条边权最大的边。因此我们先跑出最小生成树,然后对最小生成树做 LCA 的预处理,接着枚举每一条非树边,从两个端点往上跳直到 LCA 求出最大边权,然后更新答案即可。
/*
* @Author: clorf
* @Date: 2020-09-01 21:36:02
* @Last Modified by: clorf
* @Last Modified time: 2020-09-01 21:54:06
*/
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<ctime>
#define INF 1e9
using namespace std;
const int maxn=510;
const double Pi=acos(-1.0);
template<class T>void read(T &x)
{
x=0;int f=0;char ch=getchar();
while(ch<'0'||ch>'9') {f|=(ch=='-');ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return;
}
int n,m,fa[maxn],tot;
int head[maxn],cnt,dep[maxn];
long long f[maxn][35],maxx[maxn][35];
long long ans1,ans2=INF;
bool vis[maxn],flag;
struct edge
{
int x;
int y;
long long z;
}s[maxn*maxn];
struct node
{
int next;
int to;
long long num;
}e[maxn*maxn*2];
void add(int from,int to,long long num)
{
e[++cnt].next=head[from];
e[cnt].to=to;
e[cnt].num=num;
head[from]=cnt;
}
inline bool cmp(edge a,edge b)
{
return a.z<b.z;
}
int getfa(int x)
{
if(fa[x]==x)
return x;
return fa[x]=getfa(fa[x]);
}
void dfs(int u,int fa)
{
f[u][0]=fa;
dep[u]=dep[fa]+1;
for(int i=head[u];i;i=e[i].next)
{
int v=e[i].to;
if(v==fa||f[v][0])
continue;
maxx[v][0]=e[i].num;
dfs(v,u);
}
}
inline long long LCA(int x,int y)
{
long long l=0,r=0;
if(dep[x]<dep[y])
swap(x,y);
for(int i=30;i>=0;i--)
if(dep[f[x][i]]>=dep[y])
{
l=max(l,maxx[x][i]);
x=f[x][i];
}
if(x==y)
return l;
for(int i=30;i>=0;i--)
if(f[x][i]!=f[y][i])
{
l=max(l,maxx[x][i]);
r=max(r,maxx[y][i]);
x=f[x][i];
y=f[y][i];
}
l=max(l,maxx[x][0]);
r=max(r,maxx[y][0]);
return max(l,r);
}
int main()
{
while(scanf("%d%d",&n,&m)!=EOF)
{
cnt=0;
flag=0;
ans2=INF;
ans1=0;
tot=0;
memset(head,0,sizeof(head));
memset(vis,0,sizeof(vis));
memset(dep,0,sizeof(dep));
memset(f,0,sizeof(f));
memset(maxx,0,sizeof(maxx));
memset(s,0,sizeof(s));
memset(e,0,sizeof(e));
for(int i=1;i<=m;i++)
scanf("%d%d%lld",&s[i].x,&s[i].y,&s[i].z);
for(int i=1;i<=n;i++)
fa[i]=i;
sort(s+1,s+m+1,cmp);
for(int i=1;i<=m;i++)
{
int x=getfa(s[i].x);
int y=getfa(s[i].y);
if(x!=y)
{
fa[x]=y;
vis[i]=1;
add(s[i].x,s[i].y,s[i].z);
add(s[i].y,s[i].x,s[i].z);
ans1+=s[i].z;
tot++;
}
}
if(tot!=n-1)
{
ans1=-1;
flag=1;
}
dfs(1,0);
for(int j=1;j<=30;j++)
for(int i=1;i<=n;i++)
{
f[i][j]=f[f[i][j-1]][j-1];
maxx[i][j]=max(maxx[i][j-1],maxx[f[i][j-1]][j-1]);
}
for(int i=1;i<=m;i++)
if(!vis[i])
{
int x=s[i].x;
int y=s[i].y;
long long w=s[i].z;
long long num=LCA(x,y);
if(ans2>ans1-num+w)
ans2=ans1-num+w;
}
if(flag)
printf("Cost: -1\nCost: -1\n");
else if(n==m+1)
printf("Cost: %lld\nCost: -1\n",ans1);
else
printf("Cost: %lld\nCost: %lld\n",ans1,ans2);
}
return 0;
}对于严格次小生成树,为了防止非树边的权值等于最大边权的权值,即非严格次小生成树,我们还要同时预处理一个次大值。如果最大值和非树边的边权相同,就用次大值替换。
#include<cstdio>
#include<cmath>
#include<cstring>
#include<cstdlib>
#include<algorithm>
using namespace std;
long long n,m;
long long head[101010],cnt;
long long dep[101010],maxx[101010][21],minx[101010][21];//maxx[i][j]i节点到i的2^j祖先路径上最大权值,minx为次大
long long f[101010][20],fa[101010];
bool vis[301010];
long long sum;
struct node
{
long long a;
long long b;
long long num;
}s[301010];
struct edge
{
long long next;
long long to;
long long num;
}e[601010];
long long read()
{
char c;long long f=0;
for(c=getchar();c<'0'||c>'9';c=getchar());
for(;c<='9'&&c>='0';c=getchar()) f=(f<<3)+(f<<1)+c-'0';
return f;
}
bool cmp(node a,node b)
{
return a.num<b.num;
}
long long getfa(long long x)//找88
{
if(fa[x]==x)
return x;
return fa[x]=getfa(fa[x]);
}
void add(long long from,long long to,long long num)
{
e[++cnt].next=head[from];
e[cnt].to=to;
e[cnt].num=num;
head[from]=cnt;
}
void kruscal()//求最小生成树
{
sort(s+1,s+m+1,cmp);
long long temp=0;//树的边数
for(int i=1;i<=m;i++)
{
long long x=getfa(s[i].a);
long long y=getfa(s[i].b);
if(x!=y)
{
fa[x]=y;
temp++;
sum+=s[i].num;//权值
vis[i]=true;
add(s[i].a,s[i].b,s[i].num);
add(s[i].b,s[i].a,s[i].num);
}
if(temp==n-1)
break;
}
}
void dfs(long long u,long long last)//求深度和f数组初始化
{
for(int i=head[u];i;i=e[i].next)
{
long long v=e[i].to;
if(v==last)
continue;
dep[v]=dep[u]+1;
maxx[v][0]=e[i].num;
f[v][0]=u;
dfs(v,u);
}
}
void ready()//求f,maxx,minx数组
{
for(int i=1;i<=18;i++)
for(int j=1;j<=n;j++)
{
f[j][i]=f[f[j][i-1]][i-1];
maxx[j][i]=max(maxx[j][i-1],maxx[f[j][i-1]][i-1]);
minx[j][i]=max(minx[j][i-1],minx[f[j][i-1]][i-1]);
if(maxx[j][i-1]<maxx[f[j][i-1]][i-1]&&minx[j][i]<maxx[j][i-1])//判断次大是否可以更新,如果maxx更新了minx可以就更大
minx[j][i]=maxx[j][i-1];
else if(maxx[j][i-1]>maxx[f[j][i-1]][i-1]&&minx[j][i]<maxx[f[j][i-1]][i-1])
minx[j][i]=maxx[f[j][i-1]][i-1];
}
}
int LCA(long long a,long long b)//倍增求LCA
{
int i,j;
if(dep[a]<dep[b])
swap(a,b);
for(i=0;(1<<i)<=dep[a];i++);
i--;
for(j=i;j>=0;j--)
if(dep[a]-(1<<j)>=dep[b])
a=f[a][j];
if(a==b)
return a;
for(i=18;i>=0;i--)
if(f[a][i]!=f[b][i])
{
a=f[a][i];
b=f[b][i];
}
return f[a][0];
}
int find(long long a,long long b,long long lca,long long limit)//a,b,边的两个节点,lca为a,b的LCA,limit为最小生成树上最大边权值
{
int i,j;
long long l=0,r=0;
for(i=0;(1<<i)<=dep[a];i++);
i--;
for(j=i;j>=0;j--)//找从a出发到lca的最大可以替换满足要求的边
if(dep[a]-(1<<j)>=dep[lca])
{
if(maxx[a][j]!=limit)//满足要求,没超过限制
l=max(l,maxx[a][j]);
else
l=max(l,minx[a][j]);
a=f[a][j];
}
for(int i=0;(1<<i)<=dep[b];i++);//找从b出发到lca的最大可以替换满足要求的边
i--;
for(int j=i;j>=0;j--)
if(dep[b]-(1<<j)>=dep[lca])
{
if(maxx[b][j]!=limit)
r=max(r,maxx[b][j]);
else
r=max(r,minx[b][j]);
b=f[b][j];
}
return max(l,r);
}
void solve()
{
long long ans=2e+18;
for(int i=1;i<=m;i++)
if(!vis[i])
{
long long a=s[i].a;
long long b=s[i].b;
long long c=s[i].num;
long long lca=LCA(a,b);
long long temp=find(a,b,lca,c);
if(temp!=c&&ans>sum-temp+c)
ans=sum-temp+c;
}
printf("%lld",ans);
}
int main()
{
n=read();
m=read();
for(int i=1;i<=n;i++)
fa[i]=i;
for(int i=1;i<=m;i++)
{
s[i].a=read();
s[i].b=read();
s[i].num=read();
}
kruscal();
dfs(1,0);
ready();
solve();
return 0;
}例 10
最小乘积生成树。
解析:这道题需要用到一些特殊的套路。我们把每棵生成树的 和 看作一个坐标 ,那么我们就相当于找一个 最小的点。很明显,这个答案只会出现这些点的下凸包中。接着就是要求下凸包中每个点的答案的最小值。关于求凸包,我们首先要求出与 轴和 轴最近的点,即要求 或 最小,这个很简单,分别把 和 作为边权,求出来的就是与横纵轴最近的点,我们把它设为 两点。然后要求找一个在 左下方且离 最远的点 ,即要让 最大。通过向量的叉积公式可以知道:
后面两项是常数,我们只需要最小化前两项,我们把边权设为 ,然后求最小生成树即可。
最后递归处理 和 即可,当 不在 的左下角,即 时就结束即可。
/*
* @Author: clorf
* @Date: 2020-09-03 21:47:12
* @Last Modified by: clorf
* @Last Modified time: 2020-09-03 21:47:34
*/
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<ctime>
#define INF 2e18
using namespace std;
const int maxn=10010;
const double Pi=acos(-1.0);
template<class T>void read(T &x)
{
x=0;int f=0;char ch=getchar();
while(ch<'0'||ch>'9') {f|=(ch=='-');ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return;
}
int n,m,a[maxn],b[maxn];
int fa[220];
struct point
{
long long x;
long long y;
}ans;
struct edge
{
int x;
int y;
int z;
int a;
int b;
}e[maxn];
inline bool cmp(edge m,edge n)
{
return m.z<n.z;
}
int getfa(int x)
{
if(fa[x]==x)
return x;
return fa[x]=getfa(fa[x]);
}
inline point kruskal()
{
sort(e+1,e+m+1,cmp);
for(int i=1;i<=n;i++)
fa[i]=i;
int suma=0,sumb=0,tot;
for(int i=1;i<=m;i++)
{
int x=getfa(e[i].x);
int y=getfa(e[i].y);
if(x!=y)
{
fa[x]=y;
suma+=e[i].a;
sumb+=e[i].b;
tot++;
}
if(tot==n-1)
break;
}
point p;
p.x=suma;
p.y=sumb;
return p;
}
inline void compare(point b)
{
long long A=1ll*ans.x*ans.y;
long long B=1ll*b.x*b.y;
if(A>B||(A==B&&b.x<ans.x))
{
ans.x=b.x;
ans.y=b.y;
}
return ;
}
void solve(point a,point b)
{
for(int i=1;i<=m;i++)
e[i].z=(b.x-a.x)*e[i].b+(a.y-b.y)*e[i].a;
point c=kruskal();
compare(c);
if((b.x-a.x)*(c.y-a.y)-(c.x-a.x)*(b.y-a.y)>=0)
return ;
solve(a,c);
solve(c,b);
}
int main()
{
ans.x=ans.y=0x7f7f7f7f;
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
scanf("%d%d%d%d",&e[i].x,&e[i].y,&e[i].a,&e[i].b);
e[i].x++;
e[i].y++;
}
for(int i=1;i<=m;i++)
e[i].z=e[i].a;
point s=kruskal();
compare(s);
for(int i=1;i<=m;i++)
e[i].z=e[i].b;
point t=kruskal();
compare(t);
solve(s,t);
printf("%lld %lld\n",ans.x,ans.y);
return 0;
}例 11
Kruskal 重构树的运用。
解析:一道很经典的 Kruskal 重构树题目,是第一次 Kruskal 重构树出现在 NOI 的考试上。
我们把从某一点到 的路径分为两部分,前面全开车,后面全走路。那么前一部分的海拔应该全大于水位线,后面一部分都小于水位线。可以用 Kruskal 重构树来做,我们跑最大生成树,建立一个小根堆,然后通过倍增可以找到一个深度最小的恰好海拔大于水位线的临界点,那么它的子树内的全部节点都可以开车。然后我们就要求临界点这个子树内所有点的到 号节点的最短路,可以先用 Dijkstra 求出 号节点到所有节点的最短路,然后用 dfs 跑某个节点子树内的最短路(其实只用记录子树内叶子节点的最短路最小值即可,因为 Kruskal 重构树只有叶子节点是原图上的点)。
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<ctime>
#include<queue>
#define INF 1e9
using namespace std;
const int maxn=400010,maxm=800010;
const double Pi=acos(-1.0);
template<class T>void read(T &x)
{
x=0;int f=0;char ch=getchar();
while(ch<'0'||ch>'9') {f|=(ch=='-');ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return;
}
long long T,n,m,fa[maxn];
long long head[maxm],cnt,val[maxn];
long long dis[maxn],vis[maxn],tot;
long long minn[maxn],f[maxn][25];
struct edge
{
long long x;
long long y;
long long z;
}t[maxm<<1];
long long cmp(edge a,edge b)
{
return a.z>b.z;
}
struct node
{
long long next;
long long to;
long long num;
}e[maxm<<1];
void add(long long from,long long to,long long num)
{
e[++cnt].next=head[from];
e[cnt].to=to;
e[cnt].num=num;
head[from]=cnt;
}
long long getfa(long long x)
{
if(x==fa[x])
return x;
return fa[x]=getfa(fa[x]);
}
void dijkstra()
{
priority_queue<pair<long long,long long> > q;
memset(dis,0x3f,sizeof(dis));
memset(vis,0,sizeof(vis));
dis[1]=0;
q.push(make_pair(0,1));
while(!q.empty())
{
long long u=q.top().second;
q.pop();
if(vis[u])
continue;
vis[u]=1;
for(long long i=head[u];i;i=e[i].next)
{
long long v=e[i].to;
if(dis[v]>dis[u]+e[i].num)
{
dis[v]=dis[u]+e[i].num;
q.push(make_pair(-dis[v],v));
}
}
}
}
void dfs(long long u,long long fa)
{
minn[u]=dis[u];
for(long long i=head[u];i;i=e[i].next)
{
long long v=e[i].to;
if(v==fa)
continue;
f[v][0]=u;
dfs(v,u);
minn[u]=min(minn[u],minn[v]);
}
}
void kruskal()
{
memset(head,0,sizeof(head));
cnt=1;
sort(t+1,t+m+1,cmp);
for(long long i=1;i<=n;i++)
fa[i]=i;
for(long long i=1;i<=m;i++)
{
long long f1=getfa(t[i].x);
long long f2=getfa(t[i].y);
if(f1!=f2)
{
val[++tot]=t[i].z;
fa[f1]=fa[f2]=fa[tot]=tot;
add(tot,f1,0);
add(tot,f2,0);
}
}
dfs(tot,0);
}
int main()
{
read(T);
while(T--)
{
memset(head,0,sizeof(head));
cnt=1;
memset(f,0,sizeof(f));
memset(minn,0x3f,sizeof(minn));
read(n),read(m);
tot=n;
for(long long i=1;i<=m;i++)
{
long long u,v,l,a;
read(u),read(v);
read(l),read(a);
add(u,v,l);
add(v,u,l);
t[i].x=u;
t[i].y=v;
t[i].z=a;
}
dijkstra();
kruskal();
for(long long i=1;(1<<i)<=tot;i++)
for(long long u=1;u<=tot;u++)
f[u][i]=f[f[u][i-1]][i-1];
long long Q,K,S;
long long last=0;
read(Q),read(K),read(S);
while(Q--)
{
long long v,p;
read(v),read(p);
v=(v+K*last-1)%n+1;
p=(p+K*last)%(S+1);
for(long long i=22;i>=0;i--)
if(f[v][i]&&val[f[v][i]]>p)
v=f[v][i];
printf("%lld\n",last=minn[v]);
}
}
return 0;
}例 12
一定包含一条边的最小生成树,对每条边询问。
CF609E Minimum spanning tree for each edge
解析:跟次小生成树一个套路,如果这条边在最小生成树上,答案就是最小生成树,否则就向上跳 LCA,用环上最大的边换掉这条边。
/*
* @Author: clorf
* @Date: 2020-08-27 21:57:18
* @Last Modified by: clorf
* @Last Modified time: 2020-08-27 21:57:18
*/
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<ctime>
#define INF 1e9
#define int long long
using namespace std;
const int maxn=200010;
const double Pi=acos(-1.0);
template<class T>void read(T &x)
{
x=0;int f=0;char ch=getchar();
while(ch<'0'||ch>'9') {f|=(ch=='-');ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return;
}
int n,m,fa[maxn],sum;
int f[maxn][25],maxx[maxn][25],dep[maxn];
int head[maxn],cnt,ans[maxn];
bool vis[maxn];
struct edge
{
int x;
int y;
int z;
int id;
}s[maxn<<1];
struct node
{
int next;
int to;
int num;
}e[maxn<<1];
void add(int from,int to,int num)
{
e[++cnt].next=head[from];
e[cnt].to=to;
e[cnt].num=num;
head[from]=cnt;
}
bool cmp(edge a,edge b)
{
return a.z<b.z;
}
int getfa(int x)
{
if(fa[x]==x)
return x;
return fa[x]=getfa(fa[x]);
}
void dfs(int u,int pre)
{
//printf("%lld %lld\n",u,pre);
dep[u]=dep[pre]+1;
f[u][0]=pre;
//printf("%lld %lld\n",u,f[u][0]);
for(int i=head[u];i;i=e[i].next)
{
int v=e[i].to;
if(v==pre||f[v][0])
continue;
maxx[v][0]=e[i].num;
dfs(v,u);
}
}
int LCA(int x,int y)
{
if(dep[x]<dep[y])
{
x=x^y;
y=x^y;
x=x^y;
}
for(int i=20;i>=0;i--)
if(dep[f[x][i]]>=dep[y])
x=f[x][i];
if(x==y)
return x;
for(int i=20;i>=0;i--)
if(f[x][i]!=f[y][i])
{
x=f[x][i];
y=f[y][i];
}
return f[x][0];
}
int find(int x,int y,int lca)
{
int j;
int l=0,r=0;
for(j=20;j>=0;j--)
if(dep[x]-(1<<j)>=dep[lca])
{
l=max(l,maxx[x][j]);
x=f[x][j];
}
for(j=20;j>=0;j--)
if(dep[y]-(1<<j)>=dep[lca])
{
r=max(r,maxx[y][j]);
y=f[y][j];
}
return max(l,r);
}
signed main()
{
scanf("%lld%lld",&n,&m);
for(int i=1;i<=m;i++)
{
scanf("%lld%lld%lld",&s[i].x,&s[i].y,&s[i].z);
s[i].id=i;
}
sort(s+1,s+m+1,cmp);
for(int i=1;i<=n;i++)
fa[i]=i;
for(int i=1;i<=m;i++)
{
int x=getfa(s[i].x);
int y=getfa(s[i].y);
if(x!=y)
{
fa[x]=y;
add(s[i].x,s[i].y,s[i].z);
add(s[i].y,s[i].x,s[i].z);
sum+=s[i].z;
vis[i]=1;
}
}
//dep[1]=1;
dfs(1,0);
for(int j=1;j<=20;j++)
for(int i=1;i<=n;i++)
{
f[i][j]=f[f[i][j-1]][j-1];
maxx[i][j]=max(maxx[i][j-1],maxx[f[i][j-1]][j-1]);
//printf("%lld %lld %lld %lld\n",i,j,f[i][j],maxx[i][j]);
}
for(int i=1;i<=m;i++)
{
if(vis[i])
ans[s[i].id]=sum;
else
{
int x=s[i].x;
int y=s[i].y;
int lca=LCA(x,y);
int num=find(x,y,lca);
// printf("%lld %lld %lld %lld\n",x,y,lca,num);
ans[s[i].id]=sum+s[i].z-num;
}
}
for(int i=1;i<=m;i++)
printf("%lld\n",ans[i]);
return 0;
}例 13
无向带权图。每次更改一条边的权值,询问最小生成树。各询问间独立,每次询问不对之后的询问产生影响,即被更改的边在下一条询问中依然是原状。
UVA1504 Genghis Khan the Conqueror
解析:原题是保证把边改大,但可以扩展到一般情况(以下的树边都指最小生成树上的边)。
答案即为原最小生成树减去改变的差值。
答案即为原最小生成树。
设原最小生成树的总权值 ,通过例 的解法求出一定要包含这条非树边的最小生成树的总权值 ,答案即为 。
只有两种情况,第一种就是依然经过这条树边,答案即为原最小生成树加上改变的差值。第二种就是不经过这条树边,用另一条非树边替代它(就是将这条树边断掉后的两个连通块之间的边权最小的非树边)。考虑枚举每一条非树边。它所能代替的树边为它端点在生成树上的路径上的边。处理这种用非树边 更新树上 和 路径的边的问题有一个经典做法,和这道题 Safe Travel G 一模一样,我们要用最小的非树边,那我们就先将其从小到大排序,这样就保证每个树上的点第一次被更新的答案就是最优的,并且每个点只会更新唯一一次(因为并查集在更新后会把节点的代表元指向其 LCA)。接着利用并查集往上跳,同时更新答案即可。最终答案就是第一种情况和第二种情况取最小值。
/*
* @Author: clorf
* @Date: 2020-08-28 14:57:18
* @Last Modified by: clorf
* @Last Modified time: 2020-08-28 16:32:36
*/
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<ctime>
#define INF 1e9
using namespace std;
const int maxn=3010;
const double Pi=acos(-1.0);
template<class T>void read(T &x)
{
x=0;int f=0;char ch=getchar();
while(ch<'0'||ch>'9') {f|=(ch=='-');ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return;
}
int n,m,q,fa[maxn];
int head[maxn],cnt;
int pre[maxn],last[maxn],dep[maxn];
long long t[maxn];
bool map[maxn][maxn],vis[maxn];
struct edge
{
int x;
int y;
int z;
}s[maxn*maxn];
struct node
{
int next;
int to;
int num;
}e[maxn*maxn];
inline void add(int from,int to,int num)
{
e[++cnt].next=head[from];
e[cnt].to=to;
e[cnt].num=num;
head[from]=cnt;
}
inline bool cmp(edge a,edge b)
{
return a.z<b.z;
}
int getfa(int x)
{
if(fa[x]==x)
return x;
return fa[x]=getfa(fa[x]);
}
void dfs(int u)
{
dep[u]=dep[last[u]]+1;
for(int i=head[u];i;i=e[i].next)
{
int v=e[i].to;
if(v==last[u])
continue;
last[v]=u;
pre[v]=e[i].num;
dfs(v);
}
}
int main()
{
while(scanf("%d%d",&n,&m)!=EOF&&n+m)
{
cnt=0;
memset(head,0,sizeof(head));
memset(t,0x3f,sizeof(t));
memset(pre,0,sizeof(pre));
memset(last,0,sizeof(last));
memset(dep,0,sizeof(dep));
memset(map,0,sizeof(map));
long long ans=0;
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&s[i].x,&s[i].y,&s[i].z);
s[i].x++;
s[i].y++;
vis[i]=0;
}
sort(s+1,s+m+1,cmp);
for(int i=1;i<=n;i++)
fa[i]=i;
for(int i=1;i<=m;i++)
{
int x=getfa(s[i].x);
int y=getfa(s[i].y);
if(x!=y)
{
fa[x]=y;
add(s[i].x,s[i].y,s[i].z);
add(s[i].y,s[i].x,s[i].z);
ans+=s[i].z;
map[s[i].x][s[i].y]=map[s[i].y][s[i].x]=vis[i]=1;
}
}
dfs(1);
for(int i=1;i<=n;i++)
fa[i]=i;
for(int i=1;i<=m;i++)
if(!vis[i])
{
int x=getfa(s[i].x);
int y=getfa(s[i].y);
while(x!=y)
{
if(dep[x]<dep[y])
swap(x,y);
t[x]=ans+s[i].z-pre[x];
fa[x]=last[x];
x=getfa(x);
}
}
scanf("%d",&q);
long long sum=0;
for(int i=1;i<=q;i++)
{
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
u++;
v++;
if(dep[u]<dep[v])
swap(u,v);
if((!map[u][v])&&(!map[v][u]))
sum+=ans;
else
sum+=min(ans+w-pre[u],t[u]);
}
printf("%.4lf\n",(double)sum/q);
}
return 0;
}例 14
无向带权图。每次询问在图中删掉一条边后图的最小生成树。各询问间独立,每次询问不对之后的询问产生影响,即被删掉的边在下一条询问中依然存在。
解析:假设删掉的是非树边,那么答案还是最小生成树;否则解法就和上题第四种情况类似,预处理断掉某条树边的最小生成树最小值即可。注意断掉后不连通的情况(此时断掉的边就是最小生成树的必经边)和一开始图就不连通的情况。
/*
* @Author: clorf
* @Date: 2020-09-06 16:28:43
* @Last Modified by: clorf
* @Last Modified time: 2020-09-06 16:55:41
*/
// 数组一定要算好开!!!!边和点的关系
// n和m不要搞混!!!任何循环时候都要注意!!
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<ctime>
#include<queue>
#define INF 2e9
using namespace std;
const int maxn=100010;
const double Pi=acos(-1.0);
template<class T>void read(T &x)
{
x=0;int f=0;char ch=getchar();
while(ch<'0'||ch>'9') {f|=(ch=='-');ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;
return;
}
int n,m,q,tot;
int head[maxn],cnt,fa[maxn],pos[maxn];
int pre[maxn],last[maxn],dep[maxn];
long long ans,t[maxn];
bool vis[maxn],flag;
struct node
{
int next;
int to;
int num;
}e[maxn<<1];
struct edge
{
int x;
int y;
int z;
int id;
}s[maxn];
inline void add(int from,int to,int num)
{
e[++cnt].next=head[from];
e[cnt].to=to;
e[cnt].num=num;
head[from]=cnt;
}
inline bool cmp(edge a,edge b)
{
return a.z<b.z;
}
int getfa(int x)
{
if(fa[x]==x)
return x;
return fa[x]=getfa(fa[x]);
}
queue<int> que;
inline void bfs(int x)
{
que.push(x);
while(!que.empty())
{
int u=que.front();
que.pop();
dep[u]=dep[last[u]]+1;
for(int i=head[u];i;i=e[i].next)
{
int v=e[i].to;
if(v==last[u])
continue;
last[v]=u;
pre[v]=e[i].num;
que.push(v);
}
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&s[i].x,&s[i].y,&s[i].z);
s[i].id=i;
}
sort(s+1,s+m+1,cmp);
for(int i=1;i<=m;i++)
pos[s[i].id]=i;
for(int i=1;i<=n;i++)
fa[i]=i;
for(int i=1;i<=m;i++)
{
int x=getfa(s[i].x);
int y=getfa(s[i].y);
if(x!=y)
{
fa[x]=y;
ans+=s[i].z;
vis[i]=1;
add(s[i].x,s[i].y,s[i].z);
add(s[i].y,s[i].x,s[i].z);
tot++;
}
}
if(tot<n-1)
flag=1;
for(int i=0;i<=n;i++)
t[i]=INF;
bfs(1);
for(int i=1;i<=n;i++)
fa[i]=i;
for(int i=1;i<=m;i++)
if(!vis[i])
{
int x=getfa(s[i].x);
int y=getfa(s[i].y);
while(x!=y)
{
if(dep[x]<dep[y])
swap(x,y);
t[x]=ans-pre[x]+s[i].z;
fa[x]=last[x];
x=getfa(x);
}
}
scanf("%d",&q);
for(int i=1;i<=q;i++)
{
int x;
scanf("%d",&x);
if(!flag)
{
if(!vis[pos[x]])
printf("%lld\n",ans);
else
{
int u=s[pos[x]].x;
int v=s[pos[x]].y;
if(dep[u]<dep[v])
swap(u,v);
if(t[u]>=INF)
printf("Not connected\n");
else
printf("%lld\n",t[u]);
}
}
else
printf("Not connected\n");
}
return 0;
}
