2020 省选联考

A 卷 T1/B 卷 T3 冰火战士

解析：撇开花里胡哨的比赛方式，首先容易看出每次比赛的消耗的能量为当时能量和小的那一边的两倍，这是因为车轮战中，两边的能量消耗一定是相同的，而能量和小的那一方会先被打败。

由于冰系战士要求场地温度大于等于他的自身温度才能参赛，因此当场地温度变大时，冰系战士参赛的人也会越多，即冰系战士的总能量随着场地温度变大而递增。同理可得，火系战士的总能量随着场地温度变大而递减。如下图所示：

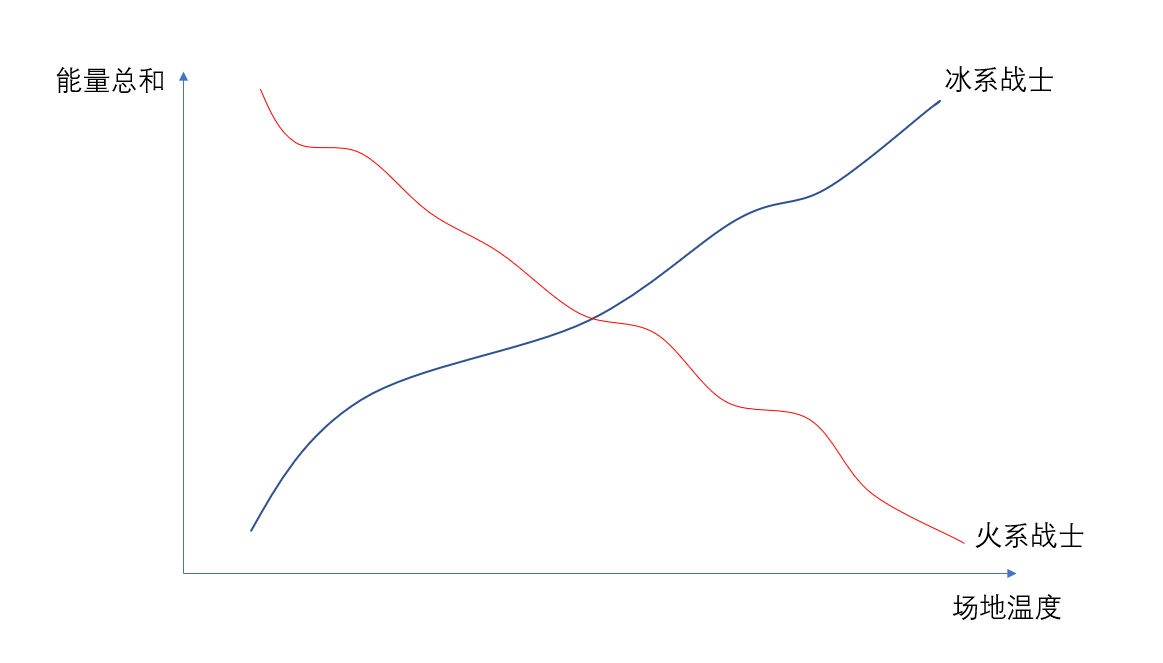
image-20210404122752339

取 min⁡\min 后，可以发现当冰系战士和火系战士的图线相交时，此时能够使得能量和较小那方的能量和最大。由于我们的温度是离散的，因此会有两个答案，设 f1(i),f2(i)f _{1}(i),f _{2}(i) 分别代表温度为 ii 时冰系战士和火系战士的能量总和，那么第一个答案即为一个最大的温度 t1t _{1} 使得 f1(t1)≤f2(t1)f _{1}(t _{1})\le f _{2}(t _{1})，第二个答案即为一个最大的温度 t2t _{2} 使得 f1(t2)≥f2(t2)f _{1}(t _{2})\ge f _{2}(t _{2})，且 f2(t2)=f2(t1+1)f _{2}(t _{2})=f _{2}(t _{1}+1)。

这下就很好处理了，我们先离散化，然后用树状数组维护 f1(i),f2(i)f _{1}(i),f _{2}(i)，然后再二分出 t1,t2t _{1},t _{2} 即可，时间复杂度为 O(Qlog⁡2Q)O(Q\log ^{2} Q)，然而依然无法拿到满分。

我们考虑直接在树状数组中二分，从大到小枚举 22 的幂次，然后依次向后跳，类似于倍增跳 LCA，因为在树状数组中，tritr _{i} 存的是 [i−lowbit(i)+1,i][i-\text{lowbit}(i)+1,i] 的区间的和，所以当 ii 增加 2j2 ^{j} 时，增加的就是后面这 2j2 ^{j} 个数的和。代码如下所示：

int now=0,sum=0;
for(int i=20;i>=-;i--)
{
    int nex=now|(1<<i);
    if(nex<=n&&sum+...)//后面为二分要的条件
    {
        sum+=...;
       	now|=(1<<i);
    }
}

然后这道题就解决了。

/*
 * @Author: clorf 
 * @Date: 2021-04-04 11:21:53 
 * @Last Modified by: clorf
 * @Last Modified time: 2021-04-04 22:08:16
 */
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<ctime>
#include<cctype>
#define INF 2e9
#define rg register
using namespace std;
const int maxn=2e6;
const long double Pi=acos(-1.0);
const double eps=1e-7;
//1.数组开小
//2.没用long long/爆了类型存储范围
//3.写之前式子没推清楚
//4.变量写错(想当然typo/没想清楚含义)
//5.写之前没想清楚复杂度
//6.常量数字与long long连用时要加ll！！！
//7.考虑无解和多解的情况
//8.两个int连成爆long long的一定要加1ll！！！！
//9.先除后乘！！！！！！
template<class T>void read(T &x)
{
    x=0;int f=0;char ch=getchar();
    while(!isdigit(ch)){f|=(ch=='-');ch=getchar();}
    while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
    x=f?-x:x;
    return;
}
int n,tot;
int op[maxn+5],type[maxn+5];
int x[maxn+5],y[maxn+5];
int b[maxn+5],f[maxn+5];
inline int lowbit(int x)
{
	return x&(-x);
}
struct BIT
{
	int tr[maxn+5],sum,cnt;
	inline void add(int x,int val)
	{
		for(int i=x;i<=tot;i+=lowbit(i))
			tr[i]+=val;
	}
	inline int query(int x)
	{
		int num=0;
		for(int i=x;i;i-=lowbit(i))
			num+=tr[i];
		return num;
	}
}ice,fire;
inline int get(int x)
{
	if(x<1||x>tot)
		return -1;
	return min(ice.query(x),fire.sum-fire.query(x-1));
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%d%d",&op[i],&type[i]);
		if(op[i]==1)
		{
			scanf("%d%d",&x[i],&y[i]);
			b[++tot]=x[i];
		}
	}
	sort(b+1,b+tot+1);
	tot=unique(b+1,b+tot+1)-b-1;
	for(int i=1;i<=n;i++)
		if(op[i]==1)
			x[i]=lower_bound(b+1,b+tot+1,x[i])-b;
	for(int i=1;i<=n;i++)
	{
		if(op[i]==1)
		{
			if(!type[i])
			{
				ice.add(x[i],y[i]);
				ice.cnt++;
				ice.sum+=y[i];
			}
			else
			{
				fire.add(x[i],y[i]);
				fire.cnt++;
				fire.sum+=y[i];
				f[x[i]]+=y[i];
			}
		}
		else
		{
			int now=type[i];
			if(!type[now])
			{
				ice.add(x[now],-y[now]);
				ice.cnt--;
				ice.sum-=y[now];
			}
			else
			{
				fire.add(x[now],-y[now]);
				fire.cnt--;
				fire.sum-=y[now];
				f[x[now]]-=y[now];
			}
		}
		if(!(ice.cnt&&fire.cnt))
		{
			puts("Peace");
			continue;
		}
		int now=0,sum1=0,sum2=0;
		for(int i=20;i>=0;i--)
		{
			int nex=now|(1<<i);
			if(nex<=tot&&sum1+ice.tr[nex]<=fire.sum-(sum2+fire.tr[nex])+f[nex])
			{
				now=nex;
				sum1+=ice.tr[nex];
				sum2+=fire.tr[nex];
			}
		}
		int ans1=get(now),ans2=get(now+1);
		if(ans1<=0&&ans2<=0)
		{
			puts("Peace");
			continue;
		}
		if(ans1>ans2)
		{
			printf("%d %d\n",b[now],ans1<<1);
			continue;
		}
		now=sum2=0;
		for(int i=20;i>=0;i--)
		{
			int nex=now|(1<<i);
			if(nex<=tot&&fire.sum-(sum2+fire.tr[nex])+f[nex]>=ans2)
			{
				now=nex;
				sum2+=fire.tr[nex];
			}
		}
		printf("%d %d\n",b[now],ans2<<1);
	}
    return 0;
}

A 卷 T2 组合数问题

解析：先推一波式子：

∑k=0nf(k)xk(nk)=∑k=0n(∑i=0maiki)xk(nk)\begin{aligned} & \sum _{k=0} ^{n}f(k)x ^{k}\dbinom{n}{k}\\ = & \sum _{k=0} ^{n}\left(\sum _{i=0} ^{m}a _{i}k ^{i}\right)x ^{k}\dbinom{n}{k}\\ \end{aligned}

然后普通幂转下降幂，这个需要用到斯特林反演，公式如下：

x ^{n}=\sum _{i} \genfrac{\{}{\}}{0}{}{n}{i}x ^{\underline{i}}

这个式子 ii 的取值范围要看 nn 与 xx 的大小关系，下界为 00，上界一般为 min⁡(n,x)\min(n,x) (其实就代表 nn 与 xx 都行，因为大于 min⁡(n,x)\min(n,x) 的部分为 00，是没有贡献的)。

设转化后 f(k)=∑i=0mbiki‾\displaystyle{f(k)=\sum _{ i=0} ^{m}b _{i}k ^{\underline{i}}}，由斯特林反演得：

\begin{aligned} f(k) & = \sum _{i=0} ^{m}a _{i}k ^{i}\\ & =\sum _{i=0} ^{m}a _{i}\sum _{j=0} ^{i}\genfrac{\{}{\}}{0}{}{i}{j}k ^{\underline{j}}\\ & =\sum _{j=0} ^{m}k ^{\underline{j}}\sum _{i=j} ^{m}\genfrac{\{}{\}}{0}{}{i}{j}a _{i} \end{aligned}

所以得到 \displaystyle{b _{i}=\sum _{j=i} ^{m}}\genfrac{\{}{\}}{0}{}{j}{i}a _{j}。上面第三步用到了和式的交换，比较显然。

然后用这个式子化简：

=∑k=0nxk∑i=0mbi(nk)ki‾\begin{aligned} = & \sum _{k=0} ^{n}x ^{k}\sum _{i=0} ^{m}b _{i}\dbinom{n}{k}k ^{\underline{i}}\\ \end{aligned}

然后用吸收公式，即：

(nm)mk‾=(n−km−k)nk‾\dbinom{n}{m}m ^{\underline{k}}=\dbinom{n-k}{m-k}n ^{\underline{k}}

可得：

=∑k=0nxk∑i=0mbi(nk)ki‾=∑k=0nxk∑i=0mbi(n−ik−i)ni‾=∑i=0mbini‾∑k=in(n−ik−i)xk\begin{aligned} = & \sum _{k=0} ^{n}x ^{k}\sum _{i=0} ^{m}b _{i}\dbinom{n}{k}k ^{\underline{i}}\\ = & \sum _{k=0} ^{n}x ^{k}\sum _{i=0} ^{m}b _{i}\dbinom{n-i}{k-i}n ^{\underline{i}}\\ = & \sum _{i=0} ^{m}b _{i}n ^{\underline{i}}\sum _{k=i} ^{n}\dbinom{n-i}{k-i}x ^{k} \end{aligned}

内层和式转为枚举 k−ik-i 可得：

=∑i=0mbini‾∑k=0n−i(n−ik)xk+i=∑i=0mbini‾xi∑k=0n−i(n−ik)xk=∑i=0mbini‾xi(x+1)n−i\begin{aligned} = & \sum _{i=0} ^{m}b _{i}n ^{\underline{i}}\sum _{k=0} ^{n-i}\dbinom{n-i}{k}x ^{k+i}\\ = & \sum _{i=0} ^{m}b _{i}n ^{\underline{i}}x ^{i}\sum _{k=0} ^{n-i}\dbinom{n-i}{k}x ^{k}\\ = & \sum _{i=0} ^{m}b _{i}n ^{\underline{i}}x ^{i}(x+1) ^{n-i}\\ \end{aligned}

然后就可以 O(m)O(m) 求出答案了。总时间复杂度为 O(m2)O(m ^{2})，复杂度瓶颈在求斯特林数以及计算 bib _{i}。

/*
 * @Author: clorf 
 * @Date: 2021-04-04 22:08:35 
 * @Last Modified by: clorf
 * @Last Modified time: 2021-04-05 17:53:28
 */
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<ctime>
#include<cctype>
#define INF 2e9
#define rg register
using namespace std;
const int maxm=1000;
const long double Pi=acos(-1.0);
const double eps=1e-7;
//1.数组开小
//2.没用long long/爆了类型存储范围
//3.写之前式子没推清楚
//4.变量写错(想当然typo/没想清楚含义)
//5.写之前没想清楚复杂度
//6.常量数字与long long连用时要加ll！！！
//7.考虑无解和多解的情况
//8.两个int连成爆long long的一定要加1ll！！！！
//9.先除后乘！！！！！！
template<class T>void read(T &x)
{
    x=0;int f=0;char ch=getchar();
    while(!isdigit(ch)){f|=(ch=='-');ch=getchar();}
    while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
    x=f?-x:x;
    return;
}
int n,x,p,m,ans;
int d[maxm+5];
int a[maxm+5],b[maxm+5];
int S[maxm+5][maxm+5];
inline int inc(int a,int b)
{
    return a+b>=p?a+b-p:a+b;
}
inline int dec(int a,int b)
{
    return a-b<0?a-b+p:a-b;
}
inline int power(int a,int b)
{
    int ans=1;
    for(;b;b>>=1)
    {
        if(b&1)
            ans=1ll*ans*a%p;
        a=1ll*a*a%p;
    }
    return ans;
}
int main()
{
    scanf("%d%d%d%d",&n,&x,&p,&m);
    for(int i=0;i<=m;i++)
        scanf("%d",&a[i]);
    S[0][0]=1;
    for(int i=1;i<=m;i++)
        for(int j=1;j<=i;j++)
            S[i][j]=inc(S[i-1][j-1],1ll*j*S[i-1][j]%p);
    for(int i=0;i<=m;i++)
        for(int j=i;j<=m;j++)
            b[i]=inc(b[i],1ll*S[j][i]*a[j]%p);
    d[0]=1;
    for(int i=1;i<=m;i++)
        d[i]=1ll*d[i-1]*(n-i+1)%p;
    for(int i=0;i<=m;i++)
        ans=inc(ans,1ll*b[i]*d[i]%p*power(x,i)%p*power(x+1,n-i)%p);
    printf("%d",ans);
    return 0;
}

A 卷 T3 魔法商店

不会保序回归，爪巴

A 卷 T4 信号传递

解析：首先对于传递序列上相邻的两个信号站 i,ji,j，可以发现对于这样一个传递，从 i→ji\to j 的代价是：

{j−ii≤jki+kji>j\begin{cases} j-i & i\le j\\ ki+kj & i>j \end{cases}

设 numi,jnum _{i,j} 代表传递序列中相邻的两个信号站为 i,ji,j 的数量，我们把这个代价分在每个点上，对于一个点 ii，设它在道路上的位置为 posipos _{i}，若 jj 在道路上的位置在 ii 之前，那么从 i→ji\to j 的代价为 posi⋅k⋅numi,jpos _{i}\cdot k\cdot num _{i,j}，从 j→ij\to i 的代价为 posi⋅numj,ipos _{i}\cdot num _{j,i}，若 jj 的位置在 ii 之后，那么从 i→ji\to j 的代价是 −posi⋅numi,j-pos _{i}\cdot num _{i,j}，从 j→ij\to i 的代价为 posi⋅k⋅numj,ipos _{i}\cdot k\cdot num _{j,i}。其实就是把上面括号中的式子拆开对应进这 44 种情况。

设 fSf _{\text{S}} 代表前 ∣S∣|\text{S}| 个位置已经填上了 S\text{S} 里面的这些数的代价，现在我们枚举 ∣S∣+1|\text{S}|+1 这个位置该填哪个数，假设加入的数为 i(i∉S)i(i\notin \text{S})，那么可以轻松写出转移式子：

fS∣i=fS+(∣S∣+1)⋅(∑j∈S(k⋅numi,j+numj,i)+∑j∉(S∣i)(−numi,j+k⋅numj,i))f _{\text{S}|i}=f _{\text{S}}+(|\text{S}|+1)\cdot\left(\sum _{j\in \text{S}}(k\cdot num _{i,j}+num _{j,i})+\sum _{j\notin (\text{S}|i)}(-num _{i,j}+k\cdot num _{j,i})\right)

枚举 S,i,j\text{S},i,j，时间复杂度为 O(2mm2)O(2 ^{m}m ^{2})，只能拿 7070 分。

考虑优化，我们对于每个集合 S\text{S}，考虑先将所有的 ii 在 S\text{S} 之后添加的代价预处理出来，记作 costS,icost _{\text{S},i}。那么转移式子就变为：

fS∣i=fS+(∣S∣+1)⋅costS,if _{\text{S}|i}=f _{\text{S}}+(|\text{S}|+1)\cdot cost _{\text{S},i}

现在思考怎么预处理 costS,icost _{\text{S},i}。我们发现可以递推，S\text{S} 可以从 S\text{S} 去掉最低位的数的状态转移过来，最低位的数为 lowbit(S)\text{lowbit(S)}，设 jj 为 lowbit(S)\text{lowbit(S)} 所代表的数，那么可以得到转移式：

costS,i=costS/j,i+(k⋅numi,j+numj,i)−(−numi,j+k⋅numj,i)cost _{\text{S},i}=cost _{\text{S}/j,i}+(k\cdot num_{i,j}+num _{j,i})-(-num _{i,j}+k\cdot num _{j,i})

其实就是把原来的 i,ji,j 的代价，即 j∉(S∣i)j\notin (\text{S}|i) 的代价减掉，再加上 j∈Sj\in\text{S} 的代价即可。

预处理和 DP 的时间复杂度都为 O(2mm)O(2 ^{m}m)，约 1.9×1081.9\times 10 ^{8}，可以接受，但是这时候 costcost 的空间复杂度也到达了 2mm2 ^{m}m 的地步，所以要继续优化空间。

我们考虑 DP 和 costcost 数组的预处理一起转移，这样每次 costcost 用到的只有两种，一种是 costS,icost _{\text{S},i}，另一种是 costS/j,icost _{\text{S}/j,i}。首先能想到的是滚动数组，按大小枚举集合，每转移完一种大小的 S\text{S} 就滚动一次。第二种就类似于 BFS，我们用 queue 每次取出队首的 S\text{S}，然后 pop 掉即可。空间的极限就是 ((2312)+(2311))⋅m\left(\dbinom{23}{12}+\dbinom{23}{11}\right)\cdot m，完全够用。

所以总空间复杂度为 2m+m⋅(mm2)2 ^{m}+m\cdot \dbinom{m}{\dfrac{m}{2}}，可以通过。

/*
 * @Author: clorf 
 * @Date: 2021-04-05 20:24:50 
 * @Last Modified by: clorf
 * @Last Modified time: 2021-04-05 21:49:21
 */
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<ctime>
#include<cctype>
#include<queue>
#define INF 2e9
#define rg register
using namespace std;
const int maxn=1e5,maxm=23;
const int maxk=100,maxlim=1<<23;
const long double Pi=acos(-1.0);
const double eps=1e-7;
//1.数组开小
//2.没用long long/爆了类型存储范围
//3.写之前式子没推清楚
//4.变量写错(想当然typo/没想清楚含义)
//5.写之前没想清楚复杂度
//6.常量数字与long long连用时要加ll！！！
//7.考虑无解和多解的情况
//8.两个int连成爆long long的一定要加1ll！！！！
//9.先除后乘！！！！！！
template<class T>void read(T &x)
{
    x=0;int f=0;char ch=getchar();
    while(!isdigit(ch)){f|=(ch=='-');ch=getchar();}
    while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
    x=f?-x:x;
    return;
}
int n,m,k,f[maxlim+5];
int s[maxn+5],cnt[maxlim+5];
int num[maxm+5][maxm+5];
int pos[maxlim+5];
struct state
{
    int now;
    int cost[maxm+5];
};
queue<state> q;
inline int lowbit(int x)
{
    return x&(-x);
}
int main()
{
    scanf("%d%d%d",&n,&m,&k);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&s[i]);
        s[i]--;
    }
    for(int i=1;i<n;i++)
        num[s[i]][s[i+1]]++;
    int lim=(1<<m)-1;
    for(int i=1;i<=lim;i++)
    {
        cnt[i]=cnt[i>>1]+(i&1);
        f[i]=INF;
    }
    state st;
    st.now=0;
    for(int i=0;i<m;i++)
    {
        st.cost[i]=0;
        pos[1<<i]=i;
        for(int j=0;j<m;j++)
        {
            if(j==i)
                continue;
            st.cost[i]-=num[i][j];
            st.cost[i]+=k*num[j][i];
        }
    }
    q.push(st);
    while(!q.empty())
    {
        state u=q.front();
        q.pop();
        int now=u.now;
        int nowp=cnt[now]+1;
        for(int T=lim^now;T;T-=lowbit(T))
        {
            int i=pos[lowbit(T)];
            f[now|(1<<i)]=min(f[now|(1<<i)],f[now]+nowp*u.cost[i]);
        }
        for(int i=0;i<m;i++)
        {
            if((now>>i)&1)
                break;
            state v;
            v.now=now|(1<<i);
            for(int T=lim^v.now;T;T-=lowbit(T))
            {
                int j=pos[lowbit(T)];
                v.cost[j]=u.cost[j]+(k*num[j][i]+num[i][j])-(k*num[i][j]-num[j][i]);
            }
            q.push(v);
        }
    }
    printf("%d",f[lim]);
    return 0;
}