最短路总结

最短路是图论的最基础算法之一，使用广泛，这篇文章主要总结最短路的套路。

需要注意的是，一般情况下在求单源最短路径的时候，一定要使用 dijkstra 算法，SPFA 已经死了(~~这个应该没人不知道吧~~)。

在此给出一些需要用到的定义。

最短路径树：一棵以起点 $s$ 为根的树，树上任意一点到 $s$ 的路径长度都等于原图中的到 $s$ 的最短路径长度。每次 dijkstra 时记录转移时每个点的前驱边，这些边即为最短路径树上的边。

最短路径图：有两种。第一种是从起点 $s$ 出发的任意一条路径长度都等于原图中最短路径的极大联通子图，第二种是从起点 $s$ 到终点 $t$ 的任意一条路径长度都等于原图中最短路径的极大联通子图。满足最短路径图一定是 DAG。

第一种在求完最短路后可以直接把每一个点往外搜一遍，如果满足 $dis_ {u}+w(u,v)=dis_ {v}$ 即是最短路径图上的边；第二种如果满足 $dis^{1}_{u}+w(u,v)+dis^{2}_{v}=dis^{1}_{t}$ 即是最短路径图上的边。

例 1

求边数最少的最短路。

解析：简单的 trick，在求最短路的同时，拿一个数组 $num_{i}$ 记录到 $i$ 的最短路的边数最小是多少，如果 $dis_{v}=dis_{u}+w(u,v)$ ，转移即为 $num_{v}=\min(num_{u}+1)$ 。

例 2

最短路条数。

Luogu1144 最短路计数

解析：基本操作，用 $cnt_{i}$ 记录到第 $i$ 个点的最短路的路径数是多少，如果 $dis_{v}=dis_{u}+w(u,v)$ ，那么转移为 $cnt_{v}=cnt_{v}+cnt_{u}$ ，否则如果 $dis_{v}>dis_{u}+w(u,v)$ ，转移则为 $cnt_{v}=cnt_{u}$ 。

#include<cstdio>
#include<cmath>
#include<queue>
#include<cstring>
#include<cstdlib>
#include<algorithm>
using namespace std;
const int mod=100003;
int n,m;
int dis[1010101],ex[1010101];
int ans[1010101],head[2010101],cnt;
struct node
{
	int next;
	int to;
}e[2010101];
void add(int from,int to)
{
	e[++cnt].next=head[from];
	e[cnt].to=to;
	head[from]=cnt;
}
void dijkstra()
{
	priority_queue< pair<int,int> > q;
	memset(dis,0x3f,sizeof(dis));
	memset(ex,0,sizeof(ex));
	ans[1]=1;
	dis[1]=0;
	q.push(make_pair(0,1));
	while(!q.empty())
	{
		int u=q.top().second;
		q.pop();
		if(ex[u])
			continue;
		ex[u]=1;
		for(int i=head[u];i;i=e[i].next)
		{
			int v=e[i].to;
			if(dis[v]>dis[u]+1)
			{
				dis[v]=dis[u]+1;
				ans[v]=ans[u]%mod;
				q.push(make_pair(-dis[v],v));
			}
			else if(dis[v]==dis[u]+1)
				ans[v]=(ans[v]+ans[u])%mod;
		}
	}
}
int main() 
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		add(x,y);
		add(y,x);
	}
	dijkstra();
	for(int i=1;i<=n;i++)
		printf("%d\n",ans[i]);
    return 0;
}

例 3

严格次短路。

Luogu2865 Roadblocks G

解析：需要在 dijkstra 的时候同时维护最短路 $dis ^{1}$ 和次短路 $dis ^{2}$ ，每次入队时如果至少能够更新次短路，那么就入队，否则就舍弃。出队时比较更新最短路和次短路即可。

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<queue>
#include<algorithm>
using namespace std;
const int maxn=1e4+101,maxm=1e5+1010;
int n,m;
int head[maxn],cnt;
int dis1[maxn],dis2[maxn],ex[maxn];
priority_queue< pair<int,int> > q;
struct node
{
	int next;
	int to;
	int num;
}e[maxm<<1];
void add(int from,int to,int num)
{
	e[++cnt].next=head[from];
	e[cnt].to=to;
	e[cnt].num=num;
	head[from]=cnt;
}
void dijkstra()
{
	memset(dis1,0x3f,sizeof(dis1));
	memset(dis2,0x3f,sizeof(dis2));
	while(!q.empty())
		q.pop();
	//dis1[1]=dis2[1]=0;
	q.push(make_pair(0,1));
	while(!q.empty())
	{
		int u=q.top().second;
		int num=-q.top().first;
		q.pop();
		if(num>=dis2[u])
			continue;
		if(num<dis1[u])
		{
			dis2[u]=dis1[u];
			dis1[u]=num;
		}
		else if(num>dis1[u]&&num<dis2[u])
			dis2[u]=num;
		for(int i=head[u];i;i=e[i].next)
		{
			int v=e[i].to;
			if(dis2[v]>num+e[i].num)
				q.push(make_pair(-num-e[i].num,v));
		}
	}
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++)
	{
		int a,b,c;
		scanf("%d%d%d",&a,&b,&c);
		add(a,b,c);
		add(b,a,c);
	}
	dijkstra();
	printf("%d",dis2[n]);
	return 0;
}

例 4

判断一条边是最短路的必经边，非必经边或不是最短路上的边。

CF567E President and Roads

解析：判断最短路的必经边有 $2$ 种方法，第一种是借助最短路径数 $cnt$ ，求出起点 $s$ 到某一点 $i$ 的最短路径数 $cnt ^{1}$ ，和某一点 $i$ 到终点 $t$ 的最短路径数 $cnt ^{2}$ ，如果当前边 $(u,v)$ 是必经边，那么它在最短路图上且满足 $cnt^{1}_{u}\times cnt^{2}_{v}=cnt^{1}_{t}$ ，非必经边就是最短路图上不满足这个条件的边。第二种方法是把最短路图建出来，利用 Tarjan 算法求桥，即是必经边。非必经边就是最短路图上的非桥边。

对于这道题，如果是必经边就直接输出 $\texttt{Yes}$ ，否则求出如果这条边在最短路图上边权应该是多少，求差值即可。

/*
 * @Author: clorf 
 * @Date: 2020-08-18 20:37:47 
 * @Last Modified by: clorf
 * @Last Modified time: 2020-08-18 22:02:26
 */
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<ctime>
#include<queue>
#define INF 1e9
using namespace std;
const int maxn=100010;
const double Pi=acos(-1.0);
template<class T>void read(T &x)
{
    x=0;int f=0;char ch=getchar();
    while(ch<'0'||ch>'9') {f|=(ch=='-');ch=getchar();}
    while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
    x=f?-x:x;
    return;
}
int n,m,s,t;
int head1[maxn],cnt1;//有向图正图
int head2[maxn],cnt2;//有向图反图
long long dis1[maxn],dis2[maxn];
long long vis[maxn];
long long num1[2][maxn],num2[2][maxn];
long long mod1=1000000009;
long long mod2=998244353;
struct node
{
    int next;
    int to;
    long long num;
}e1[maxn],e2[maxn];
struct edge
{
    int x;
    int y;
    long long z;
}e[maxn];
void add1(int from,int to,long long num)
{
    e1[++cnt1].next=head1[from];
    e1[cnt1].to=to;
    e1[cnt1].num=num;
    head1[from]=cnt1;
}
void add2(int from,int to,long long num)
{
    e2[++cnt2].next=head2[from];
    e2[cnt2].to=to;
    e2[cnt2].num=num;
    head2[from]=cnt2;
}
void dijkstra1(int x)
{
    memset(dis1,0x3f,sizeof(dis1));
    memset(vis,0,sizeof(vis));
    dis1[x]=0;
    num1[0][x]=num1[1][x]=1;
    priority_queue<pair<long long,int> > q;
    q.push(make_pair(0,x));
    while(!q.empty())
    {
        int u=q.top().second;
        q.pop();
        if(vis[u])
            continue;
        vis[u]=1;
        for(int i=head1[u];i;i=e1[i].next)
        {
            int v=e1[i].to;
            long long w=e1[i].num;
            if(dis1[v]>dis1[u]+w)
            {
                dis1[v]=dis1[u]+w;
                num1[0][v]=num1[0][u];
                num1[1][v]=num1[1][u];
                q.push(make_pair(-dis1[v],v));
            }
            else if(dis1[v]==dis1[u]+w)
            {
                num1[0][v]=(num1[0][v]+num1[0][u]+mod1)%mod1;
                num1[1][v]=(num1[1][v]+num1[1][u]+mod2)%mod2;
            }
        }
    }
}
void dijkstra2(int x)
{
    memset(dis2,0x3f,sizeof(dis2));
    memset(vis,0,sizeof(vis));
    dis2[x]=0;
    num2[0][x]=num2[1][x]=1;
    priority_queue<pair<long long,int> > q;
    q.push(make_pair(0,x));
    while(!q.empty())
    {
        int u=q.top().second;
        q.pop();
        if(vis[u])
            continue;
        vis[u]=1;
        for(int i=head2[u];i;i=e2[i].next)
        {
            int v=e2[i].to;
            long long w=e2[i].num;
            if(dis2[v]>dis2[u]+w)
            {
                dis2[v]=dis2[u]+w;
                num2[0][v]=num2[0][u];
                num2[1][v]=num2[1][u];
                q.push(make_pair(-dis2[v],v));
            }
            else if(dis2[v]==dis2[u]+w)
            {
                num2[0][v]=(num2[0][v]+num2[0][u]+mod1)%mod1;
                num2[1][v]=(num2[1][v]+num2[1][u]+mod2)%mod2;
            }
        }
    }
}
int main()
{
    scanf("%d%d%d%d",&n,&m,&s,&t);
    for(int i=1;i<=m;i++)
    {
        int a,b;
        long long c;
        scanf("%d%d%lld",&a,&b,&c);
        add1(a,b,c);
        add2(b,a,c);
        e[i].x=a;
        e[i].y=b;
        e[i].z=c;
    }
    dijkstra1(s);
    dijkstra2(t);
    for(int i=1;i<=m;i++)
    {
        int u=e[i].x;
        int v=e[i].y;
        long long w=e[i].z;
        if((dis1[u]+w+dis2[v]==dis1[t])&&((num1[0][u]*num2[0][v])%mod1==num1[0][t])&&((num1[1][u]*num2[1][v])%mod2==num1[1][t]))
            printf("YES\n");
        else
        {
            long long delta=dis1[t]-dis1[u]-dis2[v];
            if(delta<=1)
                printf("NO\n");
            else
                printf("CAN %lld\n",w-delta+1);
        }
    }
    return 0;
}

例 5

有向图/无向图求最小环。

POJ1734 Sightseeing trip

解析：对于有向图，把 $dis _{i,i}$ 赋为极大值，然后跑一边 floyd 即可，答案即为 $\displaystyle{\min_{1\le i\le n} dis_{i,i}}$ ；或者枚举起点 $s$ ，对每个起点 $s$ 跑 dijkstra， $s$ 一定是第一个被取出堆中的节点，扫描 $s$ 的所有出边，扩展完成后令 $dis[s]=+\infty$ 。如果 $s$ 第二次被堆中取出， $dis[s]$ 就是最小环的长度。对于无向图的最小环至少要 $3$ 条边，每次在 floyd 枚举中转点后转移之前，先更新答案，答案为 $\displaystyle{\min _{1\le i<j<k} dis _{i,j}+w(j,k)+w(k,i)}$ ，其中 $w(j,k)+w(k,i)$ 保证由 $j\to k\to i$ ，而 $dis _{i,j}$ 则保证由 $i\to j$ 的边不经过 $k$ ，因为 $i,j<k$ 。

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<vector>
#include<algorithm>
using namespace std;
int n,m,ans=0x3f3f3f3f;
int pos[110][110];
int a[110][110],dis[110][110];
vector<int> p;
void solve(int i,int j)
{
	if(pos[i][j]==0)
		return ;
	solve(i,pos[i][j]);
	p.push_back(pos[i][j]);
	solve(pos[i][j],j);
}
int main()
{
	scanf("%d%d",&n,&m);
	memset(a,0x3f,sizeof(a));
	for(int i=1;i<=n;i++)
		a[i][i]=0;
	for(int i=1;i<=m;i++)
	{
		int u,v,w;
		scanf("%d%d%d",&u,&v,&w);
		a[u][v]=a[v][u]=min(a[u][v],w);
	}
	memcpy(dis,a,sizeof(a));
	for(int k=1;k<=n;k++)
	{
		for(int i=1;i<k;i++)
			for(int j=i+1;j<k;j++)
				if((long long)dis[i][j]+a[j][k]+a[k][i]<ans)
				{
					ans=dis[i][j]+a[j][k]+a[k][i];
					p.clear();
					p.push_back(i);
					solve(i,j);
					p.push_back(j);
					p.push_back(k);
				}
		for(int i=1;i<=n;i++)
			for(int j=1;j<=n;j++)
				if(dis[i][j]>dis[i][k]+dis[k][j])
				{
					dis[i][j]=dis[i][k]+dis[k][j];
					pos[i][j]=k;
				}
	}
	if(ans==0x3f3f3f3f)
		printf("No solution.");
	else
		for(int i=0;i<(int)p.size();i++)
			printf("%d ",p[i]);
	return 0;
}

例 6

无向带权图，每个点 $i$ 在 $t _{i}$ 后才可以经过，多次询问两点之间在 $t$ 时刻的最短路。

Luogu1119 灾后重建

解析：由于 floyd 是通过枚举中转点依次更新最短路的，每次只能靠枚举的前 $k$ 个中转点更新路径长度。这里加入了时间点，所以依次按照时间更新中转点即可。

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
using namespace std;
int n,m,q,t[211];
int dis[210][210];
void floyd(int k)
{
	for(int i=0;i<n;i++)
		for(int j=0;j<n;j++)
			if(dis[i][j]>dis[i][k]+dis[k][j])
				dis[i][j]=dis[i][k]+dis[k][j];
	return ;
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=0;i<n;i++)
		scanf("%d",&t[i]);
	for(int i=0;i<n;i++)
		for(int j=0;j<n;j++)
			dis[i][j]=1e9;
	for(int i=0;i<n;i++)
		dis[i][i]=0;
	for(int i=1;i<=m;i++)
	{
		int a,b,c;
		scanf("%d%d%d",&a,&b,&c);
		dis[a][b]=dis[b][a]=c;
	}
	scanf("%d",&q);
	int now=0;
	for(int i=1;i<=q;i++)
	{
		int a,b,c;
		scanf("%d%d%d",&a,&b,&c);
		while(t[now]<=c&&now<n)
		{
			floyd(now);
			now++;
		}
		if(t[a]>c||t[b]>c)
		{
			printf("-1\n");
			continue;
		}
		if(dis[a][b]==1e9)
			printf("-1\n");
		else
			printf("%d\n",dis[a][b]);
	}
	return 0;
}

例 7

无向带权图。不存在异或和不为 $0$ 的环， $Q$ 次询问 $x$ 到 $y$ 的最小异或和路径。

Luogu5651 基础最短路练习题

解析：由题知，途中的环边权异或和都为 $0$ 。我们假设 $x$ 到 $y$ 的路径与某一个环相交，即如下图这种情况。

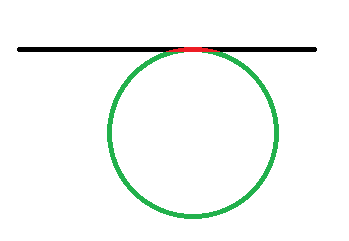
路径与环相交

其中红色路径和绿色路径即为 $x$ 到 $y$ 的两条路。我们假设 $x$ 到 $y$ 的走红色路径的异或和为 $w$ ，

那么走绿色路径的异或和就是 $w\; \text{xor}\; 0=w$ ，即选择公共路径取反的路径通过。发现两条路径的异或和相同，那么发现一条重要的结论：环上的两条路径异或和相等。因此我们任意选择一条路径通过即可，每次直接 dfs 处理。

/*
 * @Author: clorf 
 * @Date: 2020-08-23 18:41:13 
 * @Last Modified by: clorf
 * @Last Modified time: 2020-08-23 19:02:01
 */
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<ctime>
#define INF 1e9
using namespace std;
const int maxn=100010;
const double Pi=acos(-1.0);
template<class T>void read(T &x)
{
    x=0;int f=0;char ch=getchar();
    while(ch<'0'||ch>'9') {f|=(ch=='-');ch=getchar();}
    while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
    x=f?-x:x;
    return;
}
int n,m,q,dis[maxn];
int head[maxn],cnt;
bool vis[maxn];
struct node
{
    int next;
    int to;
    int num;
}e[maxn<<2];
void add(int from,int to,int num)
{
    e[++cnt].next=head[from];
    e[cnt].to=to;
    e[cnt].num=num;
    head[from]=cnt;
}
void dfs(int u)
{
    vis[u]=1;
    for(int i=head[u];i;i=e[i].next)
    {
        int v=e[i].to;
        if(vis[v])
            continue;
        dis[v]=dis[u]^e[i].num;
        dfs(v);
    }
}
int main()
{
    scanf("%d%d%d",&n,&m,&q);
    for(int i=1;i<=m;i++)
    {
        int x,y,v;
        scanf("%d%d%d",&x,&y,&v);
        add(x,y,v);
        add(y,x,v);
    }
    dfs(1);
    for(int i=1;i<=q;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        printf("%d\n",dis[x]^dis[y]);
    }
    return 0;
}

例 8

单位权无向图，可以在没有边的两点间加一条单位权边，求不影响 $s$ 到 $t$ 最短路的加边方案数。

CF954D Fight Against Traffic

解析：用 dijkstra 跑出 $s$ 和 $t$ 的单源最短路 $dis ^{1}$ 和 $dis ^{2}$ ，然后 $n ^{2}$ 枚举每个点对 $(u,v)$ ，如果 $dis ^{1} _{u}+dis ^{2} _{v}+1\ge dis _{t} ^{1}$ ，那么说明可以加边从 $u\to v$ 。

/*
 * @Author: clorf 
 * @Date: 2020-08-28 16:55:44 
 * @Last Modified by: clorf
 * @Last Modified time: 2020-08-28 17:35:13
 */
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<ctime>
#include<queue>
#define INF 1e9
using namespace std;
const int maxn=100010;
const double Pi=acos(-1.0);
template<class T>void read(T &x)
{
    x=0;int f=0;char ch=getchar();
    while(ch<'0'||ch>'9') {f|=(ch=='-');ch=getchar();}
    while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
    x=f?-x:x;
    return;
}
int n,m,s,t,dis[2][maxn],ans;
int head[maxn],cnt;
bool vis[maxn],edge[1010][1010];
struct node
{
    int next;
    int to;
}e[maxn<<1];
void add(int from,int to)
{
    e[++cnt].next=head[from];
    e[cnt].to=to;
    head[from]=cnt;
}
void dijkstra(int type,int x)
{
    priority_queue<pair<int,int> > q;
    memset(dis[type],0x3f,sizeof(dis[type]));
    memset(vis,false,sizeof(vis));
    dis[type][x]=0;
    q.push(make_pair(0,x));
    while(!q.empty())
    {
        int u=q.top().second;
        q.pop();
        if(vis[u])
            continue;
        vis[u]=1;
        for(int i=head[u];i;i=e[i].next)
        {
            int v=e[i].to;
            if(dis[type][v]>dis[type][u]+1)
            {
                dis[type][v]=dis[type][u]+1;
                q.push(make_pair(-dis[type][v],v));
            }
        }
    }
}
int main()
{
    scanf("%d%d%d%d",&n,&m,&s,&t);
    for(int i=1;i<=m;i++)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        edge[a][b]=edge[b][a]=1;
        add(a,b);
        add(b,a);
    }
    dijkstra(0,s);
    dijkstra(1,t);
    for(int i=1;i<=n;i++)
        for(int j=i+1;j<=n;j++)
        {
            if(edge[i][j])
                continue;
            if(dis[0][i]+dis[1][j]+1>=dis[0][t]&&dis[0][j]+dis[1][i]+1>=dis[0][t])
                ans++;
        }
    printf("%d\n",ans);
    return 0;
}

例 9

单位权无向图，问删除每条边后点 $1$ 到其余所有点最短路是否最多加 $1$ 。

解析：对于单位权图，并且先求出 $1$ 到其他所有点的最短路，然后直接建出 bfs 树来做。对于非树边我们可以直接删掉，对于树边我们需要先预处理一个 $cnt _{i}$ 代表树上的 $i$ 点上一层和这一层的入度数，可以直接枚举原图中每一条边 $(u,v)$ ，如果满足 $dis _{u}\le dis _{v}\le dis _{u}+1$ (其中 $dis _{v}=dis _{u}$ 说明同一层，这条边是同一层的边，否则说明是 $u$ 是 $v$ 的上一层，这条边是从上一层连下来的边)，那么 $cnt _{v}$ 加 $1$ 。对于每一条树边 $(u,v)$ 如果满足 $cnt _{v}\ge 2$ ，说明删掉这条树边后还能通过同层或上层的边到达，并且距离大小最多增加 $1$ ，所以这条树边也可以删掉。

例 10

CF715B Complete The Graph

无向带权图，给所有 $0$ 边赋值 $[1, 10 ^{18}]$ ，要求 $s$ 到 $t$ 的最短路是 $L$ ，输出方案。

解析：先把所有 $0$ 边边权赋为 $1$ ，跑一遍最短路，此时设 $s$ 到 $t$ 的最短路为 $d$ ，若 $d>L$ ，那么怎么修改边权都不能满足条件。否则设 $delta=L-d$ ，跑第 $2$ 次最短路，对于某条 $0$ 边 $(u,v)$ ，如果能够用 $dis ^{2} _{u}+w(u,v)$ 更新 $dis _{v} ^{2}$ ，可以直接先直接把 $w(u,v)$ 赋为 $dis ^{1}_{v}+delta-dis ^{2} _{u}$ ，这样每次转移都能保证让 $dis ^{2} _{v}=dis ^{1}_{v}+delta$ ，最后 $dis _{t}^{2}$ 也会加上 $delta$ ，判断是否是 $L$ 即可。

/*
 * @Author: clorf 
 * @Date: 2020-08-28 17:40:49 
 * @Last Modified by: clorf
 * @Last Modified time: 2020-08-28 17:53:54
 */
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<ctime>
#include<queue>
#define INF 1e9
using namespace std;
const int maxn=10010;
const double Pi=acos(-1.0);
template<class T>void read(T &x)
{
    x=0;int f=0;char ch=getchar();
    while(ch<'0'||ch>'9') {f|=(ch=='-');ch=getchar();}
    while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
    x=f?-x:x;
    return;
}
long long n,m,l,s,t,delta;
int head[maxn],cnt=1;
bool vis[maxn];
long long dis[2][maxn];
struct node
{
    int next;
    int to;
    long long num;
    bool flag;
}e[maxn<<1];
void add(int from,int to,long long num,bool flag)
{
    e[++cnt].next=head[from];
    e[cnt].to=to;
    e[cnt].num=num;
    e[cnt].flag=flag;
    head[from]=cnt;
}
void dijkstra(int type,int x)
{
    priority_queue<pair<long long,int> > q;
    memset(dis[type],0x3f,sizeof(dis[type]));
    memset(vis,0,sizeof(vis));
    dis[type][x]=0;
    q.push(make_pair(0,x));
    while(!q.empty())
    {
        int u=q.top().second;
        q.pop();
        if(vis[u])
            continue;
        vis[u]=1;
        for(int i=head[u];i;i=e[i].next)
        {
            int v=e[i].to;
            if(type==1)
                if(e[i].flag&&dis[0][v]+delta>dis[1][u]+e[i].num)
                    e[i].num=e[i^1].num=dis[0][v]+delta-dis[1][u];
            if(dis[type][v]>dis[type][u]+e[i].num)
            {
                dis[type][v]=dis[type][u]+e[i].num;
                q.push(make_pair(-dis[type][v],v));
            }
        }
    }
}
int main()
{
    scanf("%lld%lld%lld%lld%lld",&n,&m,&l,&s,&t);
    s++;
    t++;
    for(int i=1;i<=m;i++)
    {
        long long a,b,c;
        bool x=0;
        scanf("%lld%lld%lld",&a,&b,&c);
        a++;
        b++;
        if(!c)
        {
            x=1;
            c=1;
        }
        add(a,b,c,x);
        add(b,a,c,x);
    }
    dijkstra(0,s);
    if(dis[0][t]>l)
    {
        printf("NO");
        return 0;
    }
    delta=l-dis[0][t];
    dijkstra(1,s);
    if(dis[1][t]==l)
    {
        printf("YES\n");
        for(int i=2;i<=cnt;i+=2)
            printf("%d %d %d\n",e[i+1].to-1,e[i].to-1,e[i].num);
    }
    else
        printf("NO\n");  
    return 0;
}

例 11

给定无向图，留下最多 $k$ 条边使好点最多。称删边后到顶点最短路不变的点为好点。

CF1076D Edge Deletion

解析：直接建出最短路树，非树边可以全删完。接着如果 $k\ge n-1$ ，那么每条最短路树边都可以留下来，否则就 dfs 留下前 $k$

条树边。

/*
 * @Author: clorf 
 * @Date: 2020-08-19 17:46:16 
 * @Last Modified by: clorf
 * @Last Modified time: 2020-08-19 20:39:11
 */
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<ctime>
#include<queue>
#define INF 1e9
using namespace std;
const int maxn=300010;
const double Pi=acos(-1.0);
template<class T>void read(T &x)
{
    x=0;int f=0;char ch=getchar();
    while(ch<'0'||ch>'9') {f|=(ch=='-');ch=getchar();}
    while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
    x=f?-x:x;
    return;
}
int n,m,k,ans,step;
int head[maxn],cnt;
int vis[maxn];
long long dis[maxn];
struct node
{
    int next;
    int to;
    int num;
    int id;
}e[maxn<<1];
void add(int from,int to,int num,int id)
{
    e[++cnt].next=head[from];
    e[cnt].to=to;
    e[cnt].num=num;
    e[cnt].id=id;
    head[from]=cnt;
}
priority_queue<pair<long long,int> > q;
void dijkstra(int x)
{
    memset(dis,0x3f,sizeof(dis));
    memset(vis,0,sizeof(vis));
    dis[x]=0;
    q.push(make_pair(0,x));
    while(!q.empty())
    {
        int u=q.top().second;
        q.pop();
        if(vis[u])
            continue;
        vis[u]=1;
        for(int i=head[u];i;i=e[i].next)
        {
            int v=e[i].to;
            if(dis[v]>dis[u]+e[i].num)
            {
                dis[v]=dis[u]+e[i].num;
                q.push(make_pair(-dis[v],v));
            }
        }
    }
}
void solve(int u)
{
    vis[u]=1;
    for(int i=head[u];i;i=e[i].next)
    {
        int v=e[i].to;
        if(vis[v]||dis[v]!=dis[u]+e[i].num)
            continue;
        printf("%d ",e[i].id);
        step++;
        if(step==ans)
            exit(0);
        solve(v);
    }
}
int main()
{
    scanf("%d%d%d",&n,&m,&k);
    for(int i=1;i<=m;i++)
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        add(a,b,c,i);
        add(b,a,c,i);
    }
    ans=min(n-1,k);
    printf("%d\n",ans);
    if(!ans)
        return 0;
    dijkstra(1);
    memset(vis,0,sizeof(vis));
    solve(1);
    return 0;
}

例 12

带权无向图，给定两对起点，终点，求最短路上的最长公共路径。

Luogu2149 Elaxia的路线

解析：直接对 $4$ 个点 $s _{1},s _{2},t _{1},t _{2}$ 都跑一遍 dijkstra，然后访问每一条边 $(u,v)$ ，如果 $(u,v)$ 在 $s _{1}\to t _{1}$ 的最短路上，且在 $s _{2}\to t _{2}$ 的最短路上，就建边到图 $G _{1}$ 里，表示公共路径是同向边，否则如果 $(u,v)$ 在 $s _{1}\to t _{1}$ 的最短路上， $(v,u)$ 在 $s _{2}\to t _{2}$ 的最短路上，就建边到图 $G _{2}$ 里，表示公共路径是反向边。接着就是在两个有向图中求最长链，拓扑排序即可。

/*
 * @Author: clorf 
 * @Date: 2020-08-19 21:11:22 
 * @Last Modified by:   clorf 
 * @Last Modified time: 2020-08-19 21:11:22 
 */
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<ctime>
#include<queue>
#define INF 1e9
using namespace std;
const int maxn=500010;
const double Pi=acos(-1.0);
template<class T>void read(T &x)
{
    x=0;int f=0;char ch=getchar();
    while(ch<'0'||ch>'9') {f|=(ch=='-');ch=getchar();}
    while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
    x=f?-x:x;
    return;
}
int n,m;
int s1,t1,s2,t2,headn[maxn][2],tot[2];
int head[maxn],cnt,indgr[maxn][2],ans;
int dis[4][maxn],vis[maxn],f[maxn][2];
struct node
{
    int next;
    int to;
    int num;
}e[maxn<<1];
void add(int from,int to,int num)
{
    e[++cnt].next=head[from];
    e[cnt].to=to;
    e[cnt].num=num;
    head[from]=cnt;
}
struct newnode
{
    int next;
    int to;
    int num;
}s[maxn<<1][2];
void addnew(int from,int to,int num,int id)
{
    s[++tot[id]][id].next=headn[from][id];
    s[tot[id]][id].to=to;
    s[tot[id]][id].num=num;
    headn[from][id]=tot[id];
    indgr[to][id]++;
}
void dijkstra(int x,int type)
{
    priority_queue<pair<int,int> > q;
    memset(dis[type],0x3f,sizeof(dis[type]));
    memset(vis,0,sizeof(vis));
    dis[type][x]=0;
    q.push(make_pair(0,x));
    while(!q.empty())
    {
        int u=q.top().second;
        q.pop();
        if(vis[u])
            continue;
        vis[u]=1;
        for(int i=head[u];i;i=e[i].next)
        {
            int v=e[i].to;
            if(dis[type][v]>dis[type][u]+e[i].num)
            {
                dis[type][v]=dis[type][u]+e[i].num;
                q.push(make_pair(-dis[type][v],v));
            }
        }
    }
}
void topsort(int type)
{
    memset(f,0,sizeof(f));
    queue<int> q;
    for(int i=1;i<=n;i++)
        if(indgr[i][type]==0)
            q.push(i);
    while(!q.empty())
    {
        int u=q.front();
        q.pop();
        for(int i=headn[u][type];i;i=s[i][type].next)
        {
            int v=s[i][type].to;
            if(!(--indgr[v][type]))
                q.push(v);
            f[v][type]=max(f[v][type],f[u][type]+s[i][type].num);
            ans=max(ans,f[v][type]);
        }
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    scanf("%d%d%d%d",&s1,&t1,&s2,&t2);
    for(int i=1;i<=m;i++)
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        add(a,b,c);
        add(b,a,c);
    }
    dijkstra(s1,0);
    dijkstra(t1,1);
    dijkstra(s2,2);
    dijkstra(t2,3);
    for(int u=1;u<=n;u++)
        for(int i=head[u];i;i=e[i].next)
        {
            int v=e[i].to;
            if(dis[0][u]+e[i].num+dis[1][v]==dis[0][t1])
            {
                if(dis[2][u]+e[i].num+dis[3][v]==dis[2][t2])
                    addnew(u,v,e[i].num,0);
                if(dis[2][v]+e[i].num+dis[3][u]==dis[2][t2])
                    addnew(u,v,e[i].num,1);
            }
        }
    topsort(0);
    topsort(1);
    printf("%d\n",ans);
    return 0;
}

例 13

带权无向图， $q$ 次询问，每次询问将某一条边长度修改为 $x$ ，输出 $1\to n$ 的最短路径长度。

CF1163F Indecisive Taxi Fee

解析：分为 $4$ 种情况。

答案即为原最短路减去改变的差值。

答案即为原最短路。

设原最短路长度为 $ans$ ，修改的边为 $(u,v)$ ，答案即为 $\min(ans,\min(dis ^{1}_{u}+x+dis ^{2} _{v},dis ^{1}_{v}+x+dis ^{2} _{u})$ 。

这一种情况非常难以处理，我们先把以 $1$ 和 $n$ 为根的最短路树建出来，如图所示：

最短路树

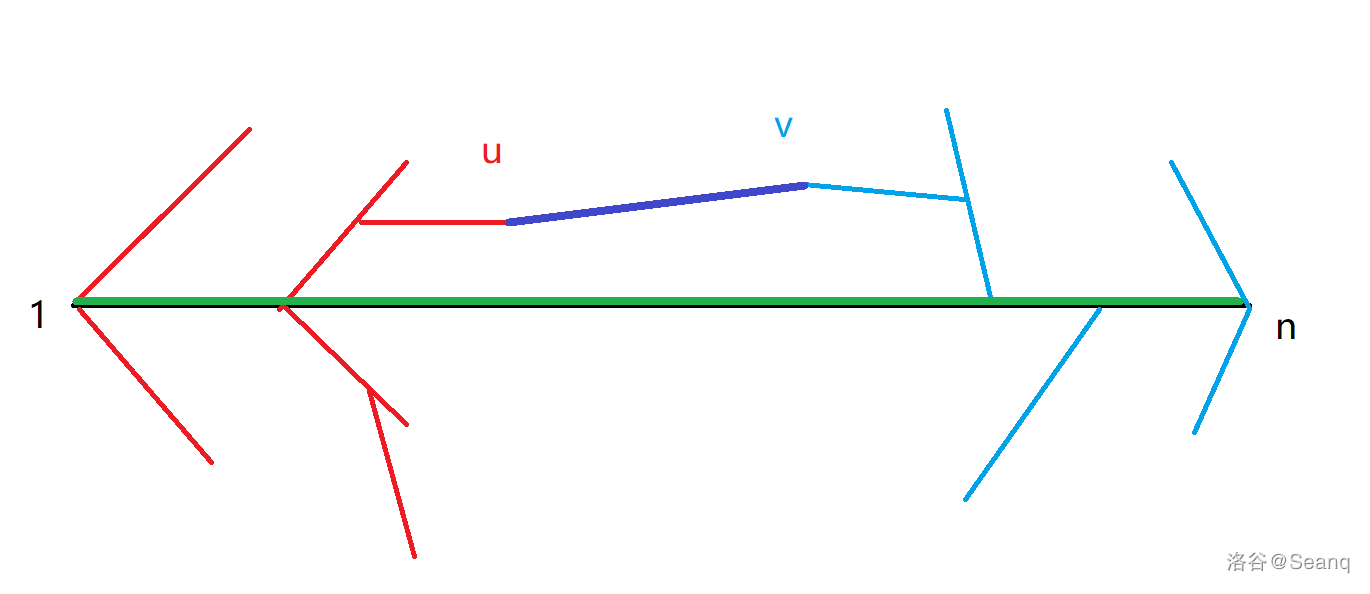
对于非树边 $(u,v)$ ，经过它的最短路一定是原最短路中的两点 $(a,b)$ ，从 $1\to a\to u\to v\to b\to n$ ，我们现在就是要求出每一个点作为 $u$ 时的 $a$ 值，记作 $l _{u}$ ，和每一个点作为 $v$ 的 $b$ 值，即 $r _{v}$ 。我们可以在 dijkstra 结束后，通过 bfs 递推从最短路径上的点 $i$ 转移出每个在最短路树上以 $i$ 为根的点的 $l,r$ 值。然后我们用一个线段树维护，线段树上每段区间 $[l,r]$ 代表不经过最短路径上 $l\to r+1$ 的最短路长度。然后对于每条非树边 $(u,v)$ ，我们把线段树上 $[l _{u},r _{v}-1]$ 用 $dis ^{1} _{u}+w(u,v)+dis ^{2} _{v}$ 更新，即每次更新取 $\min$ 值。最后要求不经过修改这条边的最短路，单点查询即可。因此维护一个支持区间取 $\min$ 和单点查询的线段树即可。

/*
 * @Author: clorf 
 * @Date: 2020-08-09 20:57:37 
 * @Last Modified by: clorf
 * @Last Modified time: 2020-08-24 21:44:33
 */
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<ctime>
#include<queue>
#define int long long
#define INF 1e9
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
using namespace std;
const int maxn=1000010;
const double Pi=acos(-1.0);
template<class T>void read(T &x)
{
    x=0;int f=0;char ch=getchar();
    while(ch<'0'||ch>'9') {f|=(ch=='-');ch=getchar();}
    while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
    x=f?-x:x;
    return;
}
int n,m,q,fa[maxn];
int head[maxn],cnt=1,l[maxn],r[maxn],path[maxn],tot;
int dis1[maxn],dis2[maxn],vis[maxn],id[maxn],book[maxn],eid[maxn];
int minn[maxn<<2],ans[maxn],tag[maxn<<2],newp,dis[maxn];
struct node
{
    int next;
    int to;
    int num;
}e[maxn<<1];
void add(int from,int to,int num)
{
    e[++cnt].next=head[from];
    e[cnt].to=to;
    e[cnt].num=num;
    head[from]=cnt;
}
void bfs(int x,int *dis,int *f)
{
    queue<int> q;
    q.push(path[x]);
    f[path[x]]=x;
    while(!q.empty())
    {
        int u=q.front();
        q.pop();
        for(int i=head[u];i;i=e[i].next)
        {
            int v=e[i].to;
            if(!f[v]&&!id[v]&&dis[u]+e[i].num==dis[v])
            {
                f[v]=x;
                q.push(v);
            }
        }
    }
}
void dijkstra(int x)
{
    memset(dis,0x3f,sizeof(dis));
    memset(vis,0,sizeof(vis));
    dis[x]=0;
    priority_queue<pair<int,int> > q;
    q.push(make_pair(0,x));
    while(!q.empty())
    {
        int u=q.top().second;
        q.pop();
        if(vis[u])
            continue;
        vis[u]=1;
        for(int i=head[u];i;i=e[i].next)
        {
            int v=e[i].to;
            if(dis[v]>dis[u]+e[i].num)
            {
                dis[v]=dis[u]+e[i].num;
                q.push(make_pair(-dis[v],v));
            }
        }
    }
}
void build(int l,int r,int rt)
{
    minn[rt]=tag[rt]=0x3f3f3f3f3f3f3f3f;
    if(l==r)
        return ;   
    int mid=(l+r)>>1;
    build(lson);
    build(rson);
}
void pushup(int rt)
{
    minn[rt]=min(minn[rt<<1],minn[rt<<1|1]);
}
void pushdown(int rt)
{
    if(tag[rt])
    {
        minn[rt<<1]=min(minn[rt<<1],tag[rt]);
        minn[rt<<1|1]=min(minn[rt<<1|1],tag[rt]);
        tag[rt<<1]=min(tag[rt<<1],tag[rt]);
        tag[rt<<1|1]=min(tag[rt<<1|1],tag[rt]);
        tag[rt]=0x3f3f3f3f3f3f3f3f;
    }
}
void update(int L,int R,int x,int l,int r,int rt)
{
    if(L<=l&&r<=R)
    {
        minn[rt]=min(minn[rt],x);
        tag[rt]=min(tag[rt],x);
        return ;
    }
    int mid=(l+r)>>1;
    pushdown(rt);
    if(L<=mid)
        update(L,R,x,lson);
    if(R>mid)
        update(L,R,x,rson);
    pushup(rt);
}
int query(int x,int l,int r,int rt)
{
    if(l==r)
        return minn[rt];
    int mid=(l+r)>>1;
    int ans=0x3f3f3f3f3f3f3f3f;
    pushdown(rt);
    if(x<=mid)
        ans=min(ans,query(x,lson));
    else
        ans=min(ans,query(x,rson));
    return ans;
}
signed main()
{
    scanf("%lld%lld%lld",&n,&m,&q);
    for(int i=1;i<=m;i++)
    {
        int a,b,c;
        scanf("%lld%lld%lld",&a,&b,&c);
        add(a,b,c);
        add(b,a,c);
    }
    dijkstra(1);
    for(int i=1;i<=n;i++)
        dis1[i]=dis[i];
    dijkstra(n);
    for(int i=1;i<=n;i++)
        dis2[i]=dis[i];
    //for(int i=1;i<=n;i++)
    //    printf("%lld %lld\n",dis1[i],dis2[i]);
    int u=1;
    while(u<n)
    {
        path[++tot]=u;
        id[u]=tot;
        for(int i=head[u];i;i=e[i].next)
        {
            int v=e[i].to;
            if(dis2[v]+e[i].num==dis2[u])
            {
                book[i]=1;
                eid[i]=tot;
                u=v;
                break;
            }
        }
    }
    path[++tot]=n;
    id[n]=tot;
    for(int i=1;i<=tot;i++)
    {
        bfs(i,dis1,l);
        bfs(i,dis2,r);
    }
    //for(int i=1;i<=n;i++)
    //    printf("%lld %lld\n",l[i],r[i]);
    tot--;
    build(1,tot,1);
    for(int u=1;u<=n;u++)
        for(int i=head[u];i;i=e[i].next)
        {
            int v=e[i].to;
            if(!book[i]&&l[u]<r[v])
                update(l[u],r[v]-1,dis1[u]+e[i].num+dis2[v],1,tot,1);
        }
    for(int i=1;i<=tot;i++)
        ans[i]=query(i,1,tot,1);
    while(q--)
    {
        int t,x;
        scanf("%lld%lld",&t,&x);
        int mich=0x3f3f3f3f3f3f3f3f;
        int u=e[t<<1|1].to;
        int v=e[t<<1].to;
        int w=e[t<<1].num;
        mich=min(dis1[u]+x+dis2[v],dis1[v]+x+dis2[u]);
        if(x>w)
        {
            if(book[t<<1])
                mich=min(mich,ans[eid[t<<1]]);
            else if(book[t<<1|1])
                mich=min(mich,ans[eid[t<<1|1]]);
            else
                mich=min(mich,dis1[n]);
        }
        else
        {
            if(book[t<<1])
                mich=min(mich,dis1[n]-w+x);
            else
                mich=min(mich,dis1[n]);
        }
        printf("%lld\n",mich);
    }
    return 0;
}

例 14

给定一张无向图，点 $s$ 到每个点最短路唯一。对于每个点，求不经过 $s$ 到其最短路上最后一条边的最短路。

Luogu2934 Safe Travel G

解析：先把最短路树建出来，如下图所示：

最短路树

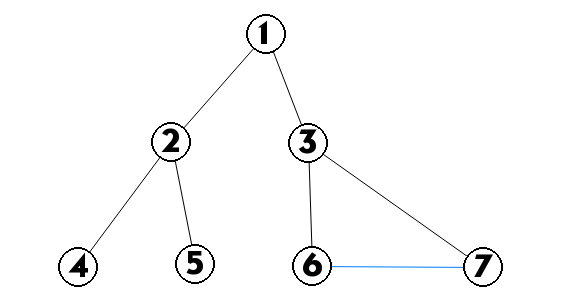
对于每条非树边(如图 $6\to 7$ )，从 $6\to \text{LCA}(u,v)=3,v\to 3$ 上的所有点( $3$ 除外)，例如 $6$ ，它本来的最短路为 $1\to 3\to 6$ ，但由于要不经过最后一条边，那么必定要经过一条非树边，经过非树边的路径为 $1\to 3\to 7\to 6$ 。扩展到一般情况，对于每条非树边 $(u,v)$ ，从 $u\to \text{LCA}(u,v),v\to \text{LCA}(u,v)$ 上的所有点( $\text{LCA}(u,v)$ 除外)，对于每个点 $i$ 的另一条路径为 $dis _{u}+dis _{v}-dis _{i}+w(u,v)$ 。发现 $dis _{i}$ 是确定的，我们只需要最小化 $dis _{u}+dis _{v}+w(u,v)$ ，直接把所有的非树边按照这个值从小到大排序，如此每个点第一次被更新的答案一定最优。接着遍历每条非树边 $(u,v)$ ，利用并查集从 $u,v$ 往上跳，同时更新答案。

/*
 * @Author: clorf 
 * @Date: 2020-08-25 10:31:44 
 * @Last Modified by: clorf
 * @Last Modified time: 2020-08-25 20:30:39
 */
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<ctime>
#include<queue>
#define INF 1e9
using namespace std;
const int maxn=500010;
const double Pi=acos(-1.0);
template<class T>void read(T &x)
{
    x=0;int f=0;char ch=getchar();
    while(ch<'0'||ch>'9') {f|=(ch=='-');ch=getchar();}
    while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
    x=f?-x:x;
    return;
}
int n,m,tot;
int head[maxn],cnt,dis[maxn],last[maxn];
int a[maxn],b[maxn],c[maxn],newp,headn[maxn];
int fa[maxn],ans[maxn],anc[maxn];
bool vis[maxn],book[maxn],mark[maxn];
struct node
{
    int next;
    int to;
    int num;
    int id;
}e[maxn<<1],t[maxn<<1];
struct point
{
    int x;
    int y;
    int z;
}s[maxn<<1];
bool cmp(point a,point b)
{
    return a.z<b.z;
}
void add(int from,int to,int num,int id)
{
    e[++cnt].next=head[from];
    e[cnt].to=to;
    e[cnt].num=num;
    e[cnt].id=id;
    head[from]=cnt;
}
void addn(int from,int to,int num)
{
    t[++newp].next=headn[from];
    t[newp].to=to;
    t[newp].num=num;
    headn[from]=newp;
}
int getfa(int x)
{
    if(fa[x]==x)
        return x;
    return fa[x]=getfa(fa[x]);
}
void dijkstra(int x)
{
    priority_queue<pair<int,int> > q;
    memset(dis,0x3f,sizeof(dis));
    memset(vis,0,sizeof(vis));
    dis[x]=0;
    q.push(make_pair(0,x));
    while(!q.empty())
    {
        int u=q.top().second;
        q.pop();
        if(vis[u])
            continue;
        vis[u]=1;
        for(int i=head[u];i;i=e[i].next)
        {
            int v=e[i].to;
            if(dis[v]>dis[u]+e[i].num)
            {
                dis[v]=dis[u]+e[i].num;
                last[v]=e[i].id;
                mark[i]=1;
                q.push(make_pair(-dis[v],v));
            }
        }
    }
}
void dfs(int u)
{
    for(int i=headn[u];i;i=t[i].next)
    {
        int v=t[i].to;
        if(v==anc[u])
            continue;
        anc[v]=u;
        dfs(v);
    }
}
int main()
{
    memset(ans,-1,sizeof(ans));
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d%d",&a[i],&b[i],&c[i]);
        add(a[i],b[i],c[i],i);
        add(b[i],a[i],c[i],i);
    }
    dijkstra(1);
    for(int i=2;i<=n;i++)
    {
        int x=last[i];
        addn(a[x],b[x],c[x]);
        addn(b[x],a[x],c[x]);
        book[x]=1;
    }
    dfs(1);
    for(int i=1;i<=m;i++)
        if(!book[i])
        {
            s[++tot].x=a[i];
            s[tot].y=b[i];
            s[tot].z=dis[a[i]]+dis[b[i]]+c[i];
        }
    sort(s+1,s+tot+1,cmp);
    for(int i=1;i<=n;i++)
        fa[i]=i;
    for(int i=1;i<=tot;i++)
    {
        int x=getfa(s[i].x);
        int y=getfa(s[i].y);
        while(x!=y)
        {
            if(dis[x]<dis[y])
                swap(x,y);
            ans[x]=s[i].z-dis[x];
            fa[x]=anc[x];
            x=getfa(x);
        }
    }
    for(int i=2;i<=n;i++)
        printf("%d\n",ans[i]);
    return 0;
}

例 15

带权有向图，从 $1$ 出发，要求必需到达 $n$ 的路径长度为 $t$ ，求出不同路径数(每一条边权值最大为 $9$ ，且为整数)。

Luogu4159 迷路

解析：假如每条边的边权都为 $1$ ，我们直接用邻接矩阵跑矩阵快速幂即可，满足

e ^{t} _{i,j}=\sum _{k=1} ^{n}e ^{t-1} _{i,k}\times e ^{1} _{k,j}

其中 $e ^{1}$ 为邻接矩阵， $e ^{i}$ 代表长度为 $i$ 的矩阵。

接着考虑 $w\in [1,9]$ 的情况，我们可以直接把点拆开，转化成边权只有 $0,1$ 的图。

把每个点拆成 $9$ 个点，令 $(i,j)$ 代表 $i$ 拆的第 $j$ 个点，只有 $(i,0)$ 是真点。我们把每一个 $(i,j)$ 都往 $(i,j-1)$ 连一条距离为 $1$ 的边。对于原图中的边 $(u,v,w)$ ，直接往 $(u,0)$ 向 $(v,w-1)$ 连一条边权为 $1$ 的边即可。这样答案就为 $e ^{t} _{(1,0),(n,0)}$ 。

/*
 * @Author: clorf 
 * @Date: 2020-08-20 19:31:48 
 * @Last Modified by: clorf
 * @Last Modified time: 2020-08-20 19:53:08
 */
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<ctime>
#define INF 1e9
using namespace std;
const int maxn=11;
const int mod=2009;
const double Pi=acos(-1.0);
template<class T>void read(T &x)
{
    x=0;int f=0;char ch=getchar();
    while(ch<'0'||ch>'9') {f|=(ch=='-');ch=getchar();}
    while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
    x=f?-x:x;
    return;
}
int n,t;
char s[maxn];
struct matrix
{
    int d[maxn*10][maxn*10];
}a;
matrix multi(matrix a,matrix b)
{
    matrix c;
    for(int i=1;i<=10*n;i++)
        for(int j=1;j<=10*n;j++)
        {
            c.d[i][j]=0;
            for(int k=1;k<=10*n;k++)
                c.d[i][j]=(c.d[i][j]+(a.d[i][k]*b.d[k][j])%mod)%mod;
        }
    return c;
}
int power(int t)
{
    matrix ans=a;
    matrix p=a;
    for(;t;t>>=1)
    {
        if(t&1)
            ans=multi(ans,p);
        p=multi(p,p);
    }
    return ans.d[1][n];
}
int main()
{
    scanf("%d%d",&n,&t);
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=8;j++)
            a.d[i+j*n][i+(j-1)*n]=1;
        scanf("%s",s+1);
        for(int j=1;j<=n;j++)
        {
            int c=s[j]-'0';
            a.d[i][j+(c-1)*n]=1;
        }
    }
    printf("%d",power(t-1));
    return 0;
}

例 16

带权无向图，求出 $s$ 到 $t$ 长度为 $w$ 的路径数，要求每条边不能走过来马上走回去。

Luogu2151 HH去散步

解析：这道题不能向上道题那样利用点的状态转移，因为要满足题目约束，不能立马来回走同一条边。

对于这种题可以利用点边互换的思想，我们用边的状态转移。邻接矩阵是如果 $i$ 点能转移到 $j$ 点，就把 $e _{i,j}$ 设为 $1$ ，我们把边编号后，如果从第 $i$ 条边能转移到第 $j$ 条边，即第 $j$ 条边的起点是 $i$ 边的终点，那么就把 $e _{i,j}$ 设为 $1$ ，注意 $i$ 由于约束条件不能是 $j$ 的反边。最后矩阵快速幂统计答案即可。

#include<stdio.h>
#include<string.h>
#include<math.h>
#include<stdlib.h>
#pragma GCC optimize (2)
#pragma G++ optimize (2)
#pragma GCC optimize("Ofast")
#pragma G++ optimize("Ofast")
long long n,m,t,a,b,u,v,next[151],to[151],cnt,mod=45989,answer;
void read(long long &x) 
{ 
	long long f=1;x=0;char s=getchar(); 
	while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();} 
	while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();} 
	x*=f; 
}
struct matrix
{
	long long map[151][151];
}ans,x,now;
matrix multi(matrix a,matrix b)
{
	matrix c=now;
	for(int i=0;i<=cnt;i++)
		for(int j=0;j<=cnt;j++)
			for(int k=0;k<=cnt;k++)
				c.map[i][j]+=(a.map[i][k]%mod*b.map[k][j]%mod)%mod;
	return c;
}
matrix power(matrix p,long long b)
{
	matrix ans=now;
	for(int i=1;i<=cnt;i++)
		ans.map[i][i]=1;
	while(b)
	{
		if(b&1)
			ans=multi(ans,p);
		p=multi(p,p);
		b>>=1;
	}
	return ans;
}
int main()
{
	read(n);
	read(m);
	read(t);
	read(a);
	read(b);
	a++;
	b++;
	next[++cnt]=0;
	to[cnt]=a;
	for(int i=1;i<=m;i++)
	{
		read(u);
		read(v);
		u++;
		v++;
		next[++cnt]=u;
		to[cnt]=v;
		next[++cnt]=v;
		to[cnt]=u;
	}
	for(int i=1;i<=cnt;i++)
		for(int j=1;j<=cnt;j++)
			if(i!=j&&i!=(j^1))
				if(to[i]==next[j])
					x.map[i][j]=1;
	ans=power(x,t);
	for(int i=1;i<=cnt;i++)
		if(to[i]==b)
			answer=(answer+ans.map[1][i])%mod;
	printf("%lld",answer);
	return 0;
}

例 17

带权有向图( $n\le 50,m\le 10000$ )， $q(q\le 10 ^{5})$ 次询问，每次询问从 $s$ 到 $t$ 至少经过 $k$ 条边的最短路。

HDU6331 Walking Plan

解析：这题比较毒瘤，要用到分块思想。我们处理出从 $i$ 到 $j$ 恰好经过 $k(k\le 100)$ 条边的最短路 $f _{k,i,j}$ 。用 $map$ 代表邻接矩阵， $dis _{i,j}$ 代表 $i$ 到 $j$ 的最短路。可得

f _{k,i,j}=\min(f _{k-1,i,l}+map _{l,j})

然后处理出从 $i$ 到 $j$ 至少经过 $k(k\le 100)$ 条边的最短路 $f ^{2}_{k,i,j}$ ，可得

f ^{2} _{k,i,j}=\min(f _{k,i,l}+dis _{l,j})

最后处理从 $i$ 到 $j$ 恰好经过 $100k(k\le 100)$ 条边的最短路 $g _{k,i,j}$ ，可得

g _{k,i,j}=\min(g _{k-1,i,l}+f _{100,l,j})

最后对于每个询问 $s,t,k$ ，枚举中转点 $j$ ，答案即为 $\min(g _{\lfloor \frac{k}{100}\rfloor,s,j}+f^{2} _{k\; \text{mod}\; 100,j,t})$ 。

/*
 * @Author: clorf 
 * @Date: 2020-08-21 20:03:13 
 * @Last Modified by: clorf
 * @Last Modified time: 2020-08-21 21:40:01
 */
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<ctime>
#define INF 1e9
using namespace std;
const int maxn=55;
const double Pi=acos(-1.0);
template<class T>void read(T &x)
{
    x=0;int f=0;char ch=getchar();
    while(ch<'0'||ch>'9') {f|=(ch=='-');ch=getchar();}
    while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
    x=f?-x:x;
    return;
}
int t,n,m,q;
int dis[maxn][maxn];
int f[105][maxn][maxn],g[105][maxn][maxn],f2[105][maxn][maxn];
//f[k][i][j]恰好k条边,g[k][i][j]恰好100k条边,f2[k][i][j]至少k条边
int main()
{
    scanf("%d",&t);
    while(t--)
    {
        read(n);
        read(m);
        memset(dis,0x3f,sizeof(dis));
        // memset(f1,0x3f,sizeof(f1));
        memset(g,0x3f,sizeof(g));
        memset(f2,0x3f,sizeof(f2));
        memset(f,0x3f,sizeof(f));
        for(int i=1;i<=m;i++)
        {
            int x,y,z;
            read(x),read(y),read(z);
            dis[x][y]=min(dis[x][y],z);
        }
        for(int i=1;i<=n;i++)
            f[0][i][i]=0;
         for(int k=1;k<=100;k++)
            for(int i=1;i<=n;i++)
                for(int j=1;j<=n;j++)
                    for(int l=1;l<=n;l++)
                        f[k][i][j]=min(f[k][i][j],f[k-1][i][l]+dis[l][j]);//恰好k条边
        for(int i=1;i<=n;i++)
            g[0][i][i]=0;
        for(int k=1;k<=100;k++)
            for(int i=1;i<=n;i++)   
                for(int j=1;j<=n;j++)
                    for(int l=1;l<=n;l++)
                        g[k][i][j]=min(g[k][i][j],g[k-1][i][l]+f[100][l][j]);//恰好100k条边
        for(int i=1;i<=n;i++)
            dis[i][i]=0;
        for(int k=1;k<=n;k++)
            for(int i=1;i<=n;i++)
                for(int j=1;j<=n;j++)
                    dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);//最短路
        for(int k=0;k<=100;k++)
            for(int i=1;i<=n;i++)   
                for(int j=1;j<=n;j++)
                    for(int l=1;l<=n;l++)
                        f2[k][i][j]=min(f2[k][i][j],f[k][i][l]+dis[l][j]);//至少k条边
        read(q);
        for(int i=1;i<=q;i++)
        {
            int s,t,k;
            read(s),read(t),read(k);
            int a=k/100;
            int b=k%100;
            int ans=0x3f3f3f3f;
            for(int j=1;j<=n;j++)
                ans=min(ans,g[a][s][j]+f2[b][j][t]);
            if(ans==0x3f3f3f3f)
                ans=-1;
            printf("%d\n",ans);
        }
    }
    return 0;
}